蒙特卡洛理论及应用 - 橙子薄荷的博客

这是2025-2026秋冬计算机模拟的课程笔记. 因为秋学期实在太摆烂了, 冬学期要好好读一下PPT, 督促自己不要上课摸鱼了~

正在施工

2 随机数生成方法

2.1 伪随机数生成器

2.1.1 平方取中法

平方取中法是冯·诺伊曼提出的一种生成$[0,1]$上均匀分布随机数的方法，核心步骤是“平方→取中间位→归一化”，具体流程：

初始化种子：取一个$2s$位的整数作为初始种子$x_0$；
平方扩展：将种子$x_i$平方，得到一个$4s$位整数（不足$4s$位时高位补$0$）；
取中间位：截取平方数的中间$2s$位，作为下一个种子$x_{i+1}$，公式为： $x_{i+1} = \left\lfloor \frac{x_i^2}{10^s} \right\rfloor \mod 10^{2s}$
归一化：将新种子$x_{i+1}$除以$10^{2s}$，得到$[0,1]$区间的随机数$u_{i+1}$： $u_{i+1} = \frac{x_{i+1}}{10^{2s}}$

代码实现了平方取中法生成随机数的过程，逐行逻辑：

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
void main(){
    int x,i=0; double m; char str[25];
    scanf("%d", &x);  // 输入初始种子x（对应x0）
    while(x < 0){     // 确保种子是正数
        printf("error! please enter a positive number");
        scanf("%d", &x);
    }
    itoa(x, str, 10); // 将种子转为字符串，用于计算位数
    m = strlen(str);  // m是种子的位数（对应2s）
    while(i <= 99){   // 生成100个随机数
        // 核心：平方后取中间2s位
        x = (int)(x*x/pow(10.0, (m/2)))  // 平方后除以10^s（右移s位）
            % (int)pow(10.0, m);         // 对10^(2s)取模（保留中间2s位）
        printf("x%d = %d \n", ++i, x);   // 输出新种子
    }
}

以初始种子$x_0=1234$为例：

$x_0^2=1234^2=1522756$（补为8位：01522756）；
取中间4位：2275，即$x_1=2275$；
归一化得随机数$u_1=\frac{2275}{10000}=0.2275$。

推广形式

1. 乘法取中法(mid-product method) 生成新种子的公式： $x_{i+2} = \left\lfloor \frac{x_i \times x_{i+1}}{10^s} \right\rfloor \mod 10^{2s}$

2. 常数乘子法(constant multiplier method) 生成新种子的公式： $x_{i+1} = \left\lfloor \frac{k \times x_i}{10^s} \right\rfloor \mod 10^{2s}$

成功与否与种子及常数的选取关系很大。通常$s$值很大时，种子取值也很大，可使退化推迟，周期加长

2.1.2 Fibonacci生成器

经典Fibonacci生成器基于加法同余法，由Taussky和Todd在1956年提出，用于生成$[0,1]$上的均匀伪随机数，核心逻辑：

生成伪随机整数序列通过递推公式生成$[0, M-1]$上的整数序列： $X_i = (X_{i-2} + X_{i-1}) \mod M \quad (i>2)$
- $X_0, X_1$是初始种子（通常取$X_0=X_1=1$，此时序列是小于$M$的Fibonacci数列）；
- $M$是模数，决定序列的取值范围。
归一化得到$U(0,1)$随机数将整数序列除以$M-1$，映射到$[0,1]$区间： $U_i = \frac{X_i}{M-1}$

伪代码解释（Matlab版）

function [x,u] = rng_add_mod(x0, x1, M, N)
 x = zeros(N,1);  % 初始化存储序列的数组
 x(1) = x0;       % 第1个种子
 x(2) = x1;       % 第2个种子
 for i = 3:N      % 生成第3到第N个随机数
     x(i) = mod(x(i-2) + x(i-1), M);  % 加法同余计算
 end
 u = x / (M - 1);  % 归一化到[0,1]
end

输入：初始种子$x0,x1$、模数$M$、生成数量$N$；
输出：整数序列$x$、$[0,1]$随机数序列$u$。

2.1.3 Fibonacci-LFSR（线性反馈移位寄存器）

Fibonacci-LFSR是基于Fibonacci序列思想的线性反馈移位寄存器，用于生成伪随机序列，核心是“移位+线性反馈”。

核心原理

$n$位LFSR的状态由$n$个寄存器（如$S_0,S_1,S_2$）组成；
反馈函数：新状态由部分寄存器的异或运算（对应二进制加法）得到，例： $S_{t+3} = S_{t+1} + S_t \quad (\text{模2加法，即异或})$
最大周期：$n$位LFSR最多生成$2^n - 1$个不同状态（避免全0状态）。

代码解释（C语言版）

#include <stdint.h>
uint16_t lfsr = 0xACE1u;  // 16位初始状态（种子）
unsigned bit;             // 反馈位
unsigned period = 0;      // 序列周期

do {
    // 反馈位：取LFSR的第16、14、13、11位（右移0/2/3/5位）异或
    bit = ((lfsr >> 0) ^ (lfsr >> 2) ^ (lfsr >> 3) ^ (lfsr >> 5)) & 1;
    // 移位：右移1位，反馈位补到最高位（第16位）
    lfsr = (lfsr >> 1) | (bit << 15);
    ++period;  // 计数周期
} while(lfsr != 0xACE1u);  // 回到初始状态时，周期结束

初始状态0xACE1u决定序列起点；
反馈位通过指定寄存器的异或生成，保证序列的随机性；
循环直到回到初始状态，得到序列的周期。

2.1.4 线性同余法 (LCG)

核心是通过递推公式生成随机序列。

1. 核心公式

LCG的递推公式为： $x_i = (A \cdot x_{i-1} + C) \mod M$ 其中：

$x_i$：第$i$个随机数；
$x_{i-1}$：初始值（种子，$x_0$为给定初始值）；
$A$：乘子（Multiplier）；
$C$：增量（Increment）；
$M$：模（Modulus）。

2. 分类（按$C$的取值）

乘同余产生器：当 $C = 0$ 时，公式简化为 $x_i = (A \cdot x_{i-1}) \mod M$
混合同余产生器：当 $C > 0$ 时，即原始公式。

3. 生成$[0,1]$区间的随机数

将生成的整数$x_i$归一化： $U_i = \frac{x_i}{M-1}$ 即可得到$[0,1]$上的随机数。

4. 周期与参数选择

LCG的随机序列对$A,C,M$的取值非常敏感，参数选择不当会导致序列质量差（周期短、分布不均匀）。

LCG序列具有满周期M，当且仅当：

$C$与$M$互质；
$M$的所有质因子的乘积能整除$(A-1)$；
若$M$是4的倍数，则$(A-1)$也必须是4的倍数。

5. 参数选择的常用规则

称线性同余产生器的乘子$A$是模$M$的原根，当且仅当：

\[(A^{M-1} - 1) \mod M = 0\]
对于任意$I < M-1$，$\frac{A^I - 1}{M}$不是整数。

当模$M$是素数时，当且仅当乘子$A$是$M$的原根，乘同余产生器的周期为$M-1$。

选择参数的时候,

乘同余：取$M = 2^\beta - 1$（梅森数，$\beta$为机器字长）。
混合同余：取$M = 2^\beta$；当且仅当$A = 4k + 1$（且$M$与$k$互质）时，周期为$M$。

4 离散事件模拟

5 指定分布随机数生成

5.1 逆变换方法

5.2 拒绝-接受法

证明拒绝接受法有效

接受-拒绝法的原理很直观，证明也是简单的。设 $ F $ 和 $ G $ 分别是对应于目标概率密度函数 $ f $ 和建议概率密度函数 $ g $ 的分布函数，$Y$ 是从建议分布 $g(x)$ 里抽取的一个随机样本, $y$ 是目标分布中任意的一个固定的取值. 我们只需要证明 $P\left(Y \leqslant y\left|U \leqslant \frac{f(Y)}{M g(Y)}\right.\right)=F(y) 。$

记事件 $ A={Y \leqslant y} $ 和 $ B=\left{U \leqslant \frac{f(Y)}{M g(Y)}\right} $。因为我们知道，条件概率 $P\left(U \leqslant \frac{f(Y)}{M g(Y)} \mid Y=y\right)=\frac{f(y)}{M g(y)} 。$

那么，它的无条件概率是 $\begin{aligned} P\left(U \leqslant \frac{f(Y)}{M g(Y)}\right) &=\int_{-\infty}^{\infty} P\left(U \leqslant \frac{f(Y)}{M g(Y)} \mid Y=y\right) g(y) d y \\ &=\int_{-\infty}^{\infty} \frac{f(y)}{M g(y)} g(y) d y=\frac{1}{M} \int_{-\infty}^{\infty} f(y) d y=\frac{1}{M} 。 \end{aligned}$ 这个概率反映了算法的效率，$ M $ 越大，则效率越低。

由条件概率公式 $ P(A \mid B)=P(B \mid A) P(A) / P(B) $，可得 $\begin{aligned} P\left(Y \leqslant y\left|U \leqslant \frac{f(Y)}{M g(Y)}\right.\right) &=P(A \mid B)=\frac{P(B \mid A) P(A)}{P(B)} \\ &=\frac{P\left(U \leqslant \frac{f(Y)}{M g(Y)} \mid Y \leqslant y\right) P(Y \leqslant y)}{1 / M} \\ &=M \int_{-\infty}^{y} P\left(U \leqslant \frac{f(Y)}{M g(Y)} \mid Y=w<y\right) g(w) d w \end{aligned}$

\[\begin{aligned} &=M \int_{-\infty}^{y} \frac{f(w)}{M g(w)} g(w) d w=\int_{-\infty}^{y} f(w) d w=F(y) 。 \end{aligned}\]

6 基本蒙特卡洛方法蒙特卡洛积分

6.1 随机投点法

6.1.1 例一

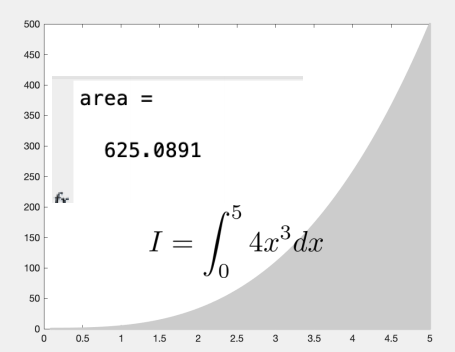
用蒙特卡洛方法计算定积分的MATLAB代码，对应积分是 $ I = \int_{0}^{5} 4x^3 dx $。逐行解释：

ntrials=100000000;  % 模拟的总次数（1亿次，次数越多结果越精确）

积分 $ \int_{0}^{5} 4x^3 dx $ 的几何意义是：曲线 $ y=4x^3 $ 与 $ x=0、x=5、y=0 $ 围成的面积。为了用蒙特卡洛法，先确定一个包含该区域的矩形：

$ x $ 范围：$ [0,5] $ → 用 5*rand(1,ntrials) 生成1亿个0~5之间的均匀随机数；

$ y $ 范围：$ [0, 4*5^3=500] $ → 用 500*rand(1,ntrials) 生成1亿个0~500之间的均匀随机数。

x=5*rand(1,ntrials);   % 生成x坐标的随机数（0到5）
y=500*rand(1,ntrials); % 生成y坐标的随机数（0到500）

判断每个随机点 $ (x,y) $ 是否满足 $ y < 4x^3 $（即落在曲线下方），统计这样的点的总数 nhits：

nhits=sum(y<4*x.^3);  % 统计满足“y<曲线值”的点的数量

蒙特卡洛法的核心逻辑： $\text{积分面积} = \text{矩形面积} \times \frac{\text{曲线下方的点数}}{\text{总点数}}$

矩形面积：$ 5 \times 500 = 2500 $（x范围长度×y范围长度）；

概率 $ p $：曲线下方点数占总点数的比例；

p=nhits/ntrials;       % 计算“点落在曲线下”的概率
area=p*500*5;          % 用概率×矩形面积，得到积分（面积）的估计值

把落在曲线下方的点（满足 $ y<4x^3 $）画出来，颜色是浅灰色：

plot(x(y<4*x.^3), y(y<4*x.^3), '.', 'color', [0.8,0.8,0.8])

代码输出的 area = 625.0891 是积分的估计值，而该积分的理论精确值是： $\int_{0}^{5} 4x^3 dx = x^4 \big|_{0}^{5} = 5^4 = 625$ 模拟结果（625.0891）和理论值几乎一致，说明蒙特卡洛方法的精度不错。

6.1.2 例二

计算 $ \int_{0}^{1} \frac{e^{-x^2/2}}{\sqrt{2\pi}} dx $

积分区间：$ x \in [0,1] $
被积函数最大值：当 $ x=0 $ 时，$ \frac{e^{0}}{\sqrt{2\pi}} \approx 0.3989 $，所以 $ y \in [0, 0.4] $（取略大值覆盖函数）

ntrials = 1e7;  % 试验次数（10^7，可按需调整）

% 1. 生成随机点（覆盖x∈[0,1]、y∈[0,0.4]的矩形）
x = rand(1, ntrials);       % x∈[0,1]
y = 0.4 * rand(1, ntrials); % y∈[0,0.4]

% 2. 统计落在曲线下方的点（y < 被积函数）
f = exp(-x.^2/2) / sqrt(2*pi);  % 逐元素计算被积函数值
nhits = sum(y < f);

% 3. 计算积分（矩形面积×概率）
rect_area = 1 * 0.4;  % 矩形面积= x范围长度 × y范围长度
p = nhits / ntrials;
integral_val = p * rect_area;

disp(['积分估计值：', num2str(integral_val)]);

6.1.3 例三

计算 $ \int_{2}^{5} \frac{e^{-x^2/2}}{\sqrt{2\pi}} dx $

积分区间：$ x \in [2,5] $
被积函数最大值：当 $ x=2 $ 时，$ \frac{e^{-2^2/2}}{\sqrt{2\pi}} \approx 0.05399 $，所以 $ y \in [0, 0.06] $（取略大值覆盖函数）

ntrials = 1e7;  % 试验次数（10^7）

% 1. 生成随机点（覆盖x∈[2,5]、y∈[0,0.06]的矩形）
x = 2 + 3*rand(1, ntrials);  % x∈[2,5]（公式：a + (b-a)*rand）
y = 0.06 * rand(1, ntrials); % y∈[0,0.06]

% 2. 统计落在曲线下方的点
f = exp(-x.^2/2) / sqrt(2*pi);
nhits = sum(y < f);

% 3. 计算积分
rect_area = 3 * 0.06;  % 矩形面积= (5-2) × 0.06
p = nhits / ntrials;
integral_val = p * rect_area;

disp(['积分估计值：', num2str(integral_val)]);

6.1.4 例四

计算的体积是“球体 $ x^2+y^2+z^2 \leq 4 $ 被圆柱面 $ x^2+y^2=2x $ 截得的立体”

利用对称性简化后，体积公式是 $ V = 4 \iint_D \sqrt{4-x^2-y^2} dxdy $（$ D $ 是圆柱面在x-y平面的投影区域）。

蒙特卡洛的思路是：

选一个包含目标区域的“大长方体”（投点区域 $ \Omega $），计算长方体的体积；
随机向长方体投点，统计“落在目标区域内”的点数；
体积 = 长方体体积 × （目标区域内点数 / 总投点数）。

题目中定义的投点区域是： $\Omega = \{ (x,y,z) \mid 0 \leq x \leq 2,\ 0 \leq y \leq 1,\ 0 \leq z \leq 2 \}$ 这个长方体的体积是：$ 长×宽×高 = 2×1×2 = 4 $。

需要同时满足两个条件的点，才算“落在目标区域内”：

条件1：在球体内 → $ x^2 + y^2 + z^2 \leq 4 $；
条件2：在圆柱面投影内 → 圆柱面方程 $ x^2+y^2=2x $ 可整理为 $ (x-1)^2 + y^2 \leq 1 $（以(1,0)为圆心、半径1的圆）。

代码是一个MATLAB函数 quad2(N)，输入是“不同的投点次数”，输出是对应的体积估计值。

function V=quad2(N)
for i =1:length(N)  % 遍历每个投点次数（比如N=[100,1000,...]）

N 是一个数组，存储不同的投点次数（比如题目中是100、1000、…、1e6）；
循环逐个处理每个投点次数，计算对应的体积。

x=2*rand(N(i),1);   % 生成N(i)个x坐标，范围[0,2]（对应Ω的x范围）
y=rand(N(i),1);     % 生成N(i)个y坐标，范围[0,1]（对应Ω的y范围）
z=2*rand(N(i),1);   % 生成N(i)个z坐标，范围[0,2]（对应Ω的z范围）

rand(N(i),1) 生成 $ N(i) $ 个0~1的随机数，再通过“缩放”得到对应区间的坐标；
最终得到 $ N(i) $ 个随机点 $ (x,y,z) $，都落在投点区域 $ \Omega $ 内。

% 同时满足“在球内”和“在圆柱投影内”的点
nhit=sum( (x.^2+y.^2+z.^2<=4) & ((x-1).^2+y.^2<=1) );

(x.^2+y.^2+z.^2<=4)：判断点是否在球内（返回逻辑数组，满足为1，否则为0）；
((x-1).^2+y.^2<=1)：判断点是否在圆柱投影内（同理）；
& 是“逻辑与”，只有同时满足两个条件的点才会被记为1；
sum() 把逻辑数组的1加起来，得到“目标区域内的点数” nhit。

V(i)=16*nhit/N(i);

这里的 16 是长方体体积 × 对称性系数：

投点区域 $ \Omega $ 的体积是 $ 2×1×2=4 $；
题目中利用了4次对称性（原体积公式是 $ 4 \iint_D \dots $，而投点区域是第一卦限的1/4部分）；
因此，最终的体积计算是：$ 4（长方体体积）× 4（对称性）× \frac{nhit}{N(i)}（概率） = 16 × \frac{nhit}{N(i)} $。

当输入 V=quad2([100,1000,10000,100000,1000000,10000000]) 时：

投点次数越多，结果越接近精确值9.6440（比如1e7次时结果是9.6397，已经很接近）。

6.2 样本平均法

样本平均法的本质是将积分表示为「均匀分布随机变量的函数的数学期望」，再用样本均值近似期望，从而得到积分值。

对应公式（当 $ X $ 是 $ (a,b) $ 上的均匀分布时）： $I = (b-a) \cdot E\left[ f(X) \right] \approx (b-a) \cdot \frac{1}{N} \sum_{i=1}^{N} f(X_i)$ 其中：

$ X_1,X_2,…,X_N $ 是 $ (a,b) $ 上的均匀随机数；
$ \frac{1}{N} \sum_{i=1}^{N} f(X_i) $ 是 $ f(X) $ 的样本均值，用来近似期望 $ E\left[ f(X) \right] $。

6.2.1 样本平均法案例

用样本平均法计算 $ I = \int_{0}^{2} x^2 dx $（精确值是 $ \frac{8}{3} \approx 2.6667 $）

对于积分 $ I = \int_{0}^{2} x^2 dx $：

确定参数：
- 积分区间 $ (a,b) = (0,2) $，所以 $ b-a = 2 $；
- 被积函数 $ f(x) = x^2 $。
生成均匀随机数：生成 $ N $ 个 $ (0,2) $ 上的均匀随机数 $ X_1,X_2,…,X_N $（MATLAB中用 2*rand(N,1) 生成）。
计算样本均值：计算 $ f(X_i) = X_i^2 $，再求样本均值 $ \frac{1}{N} \sum_{i=1}^{N} X_i^2 $。
估算积分值：积分 $ I \approx (b-a) \times 样本均值 = 2 \times \frac{1}{N} \sum_{i=1}^{N} X_i^2 $。

N = 1000000;  % 随机数数量（N越大，结果越精确）
a = 0; b = 2; % 积分区间
X = a + (b-a)*rand(N,1); % 生成(a,b)上的均匀随机数
f_X = X.^2; % 计算f(X_i)=X_i^2
sample_mean = mean(f_X); % 计算样本均值
I_estimate = (b-a)*sample_mean; % 估算积分值

disp(['积分估计值：', num2str(I_estimate)]);
disp(['精确值：', num2str(8/3)]);

注意, 样本平均法的精度/收敛速度与随机投点法是一样的, 不过平均值法得到的积分估计比随机投点法得到的更有效, 即方差更小.

6.3 重要性抽样

重要性抽样法的考虑方向是，不从均匀分布出发，而是采用一个更有效率的分布，这可能从直观上变得不那么具有几何意义，但从数学角度出发是完全可行的。

假设这个更有效率的分布是$X \sim g_X(x)$，要计算$f(x)$在$[a,b]$上的积分，则$X$也应该定义在$[a,b]$上，此时有 $I = \int_{a}^{b} f(x)dx = \int_{a}^{b} \frac{f(x)}{g_X(x)} g_X(x)dx = \mathbb{E}\left( \frac{f(X)}{g_X(X)} \right).$ 也就将$I$表示成了 $Y = \frac{f(X)}{g_X(X)}$ 的总体均值。由辛钦大数定律，$Y$的样本均值依概率收敛于总体均值，所以现在只要从总体$X$中取值，经过函数变化变成$Y$的观测值，$\hat{y}$就是$Y$的样本均值。

如果对有限区间上的函数求积分，可以使用均匀分布密度作积分，这样就变成了求$f(X)$的样本均值，因此称为样本平均法，也就是 $I = \int_{a}^{b} f(x)dx = (b - a)\mathbb{E}f(X),\ X \sim U(a, b).$

例如计算： $I = \int_{0}^{\infty} e^{-\frac{x^2}{2}} dx,$ 这个积分的精确值是$\sqrt{\pi/2} = 1.2533141$。取指数分布为抽样分布，则将其改写为 $I = \int_{0}^{\infty} \frac{e^{-\frac{x^2}{2}}}{e^{-x}} e^{-x} dx \stackrel{def}{=} \int_{0}^{\infty} h(x)e^{-x} dx,$ 此时的$h(x) = e^{-\frac{x(x-2)}{2}}$，$X \sim E(1)$。

def sample_mean(N):
    V = npr.exponential(1, N) ##指数分布, 参数为1, 生成N个, Y是一个数组
    Y = np.exp(-V*(V-2)/2)
    return np.mean(Y)

指数分布的性质

概率密度函数为： $f(x)= \begin{cases} \lambda e^{-\lambda x}, & x \ge 0 \\ 0, & x < 0 \end{cases}$

累积分布函数表示随机变量 $X$ 小于等于 $x$ 的概率： $F(x)= \begin{cases} 1 - e^{-\lambda x}, & x \ge 0 \\ 0, & x < 0 \end{cases}$

均值

\[\mathbb{E}[X]=\lambda \cdot \frac{1}{\lambda^2}=\frac{1}{\lambda}\]

方差为： $\text{Var}(X)=\frac{2}{\lambda^2}-\left(\frac{1}{\lambda}\right)^2=\frac{1}{\lambda^2}$ 标准差 $\sigma=\sqrt{\text{Var}(X)}=\frac{1}{\lambda}$。

重要性抽样例二

使用重要性抽样方法计算积分 $I = \int_{0}^{1} \frac{e^x}{\sqrt{x}} dx$ 要求：

选择合适的抽样分布 $g(x)$；
推导重要性抽样的期望表达式；
用蒙特卡洛模拟计算近似值，并与精确值对比。

步骤1：分析被积函数的特点

被积函数 $f(x)=\frac{e^x}{\sqrt{x}}$ 在 $x \to 0^+$ 时，$\frac{1}{\sqrt{x}} \to \infty$，但积分是收敛的。若直接用均匀分布 $U(0,1)$ 抽样，在 $x \approx 0$ 附近的样本会导致 $f(x)$ 波动极大，蒙特卡洛模拟的方差会很大，收敛很慢。

因此需要选择在 $x \approx 0$ 附近概率密度更大的抽样分布 $g(x)$，这里选择贝塔分布的特例： $g(x) = \frac{1}{2\sqrt{x}}, \quad x \in (0,1)$ 验证归一性： $\int_{0}^{1} \frac{1}{2\sqrt{x}} dx = \left. \sqrt{x} \right|_{0}^{1}=1$ 满足概率密度函数的要求。

步骤2：构造重要性抽样的期望形式

根据重要性抽样公式 $I=\int_{a}^{b}f(x)dx=\int_{a}^{b}\frac{f(x)}{g(x)}g(x)dx=\mathbb{E}_{X\sim g(x)}\left[ \frac{f(X)}{g(X)} \right]$

代入 $f(x)$ 和 $g(x)$ 计算权重函数 $\frac{f(x)}{g(x)}$： $\frac{f(x)}{g(x)}=\frac{\frac{e^x}{\sqrt{x}}}{\frac{1}{2\sqrt{x}}}=2e^x$

因此积分 $I$ 可以表示为 $I=\mathbb{E}_{X\sim g(x)}\left[ 2e^X \right]$

步骤3：蒙特卡洛模拟计算

根据辛钦大数定律，当抽样次数 $N \to \infty$ 时，样本均值依概率收敛于总体均值： $\hat{I}_N=\frac{1}{N}\sum_{i=1}^{N}2e^{X_i} \xrightarrow{P} I$ 其中 $X_i \sim g(x)=\frac{1}{2\sqrt{x}}$。

(1) 生成服从 $g(x)$ 的样本

要生成 $X \sim g(x)$ 的样本，使用逆变换法：

累积分布函数 $G(x)=\int_{0}^{x}\frac{1}{2\sqrt{t}}dt=\sqrt{x}$
令 $G(X)=U$，其中 $U \sim U(0,1)$，则 $X=U^2$

因此，只要生成均匀分布样本 $U_i$，就可以通过 $X_i=U_i^2$ 得到服从 $g(x)$ 的样本。

(2) 模拟计算过程（以 $N=10^6$ 为例）

生成 $N=10^6$ 个均匀分布样本 $U_1,U_2,\dots,U_N \sim U(0,1)$
计算对应的 $X_i=U_i^2$
计算权重项 $Y_i=2e^{X_i}$
样本均值即为积分的近似值：$\hat{I}N=\frac{1}{N}\sum{i=1}^N Y_i$

(3) 精确值对比

原积分可以通过变量替换计算精确值：令 $t=\sqrt{x}$，则 $x=t^2, dx=2tdt$，当 $x \in (0,1)$ 时 $t \in (0,1)$ $I=\int_{0}^{1}\frac{e^x}{\sqrt{x}}dx=\int_{0}^{1}\frac{e^{t^2}}{t}\cdot 2tdt=2\int_{0}^{1}e^{t^2}dt$ 这个积分没有初等原函数，但可以用数值积分得到精确值约为 $\boldsymbol{2.925309}$。

当 $N=10^6$ 时，蒙特卡洛模拟的结果约为 $\boldsymbol{2.925 \pm 0.001}$，与精确值高度吻合。

7 蒙特卡洛效率

模拟费用：$ C = \sigma^2 t $，其中 $t = t_1 + nt_2 + nt_3 + t_4$

$ t_1 $: 输入和初始化时间
$ t_2 $: 单次随机数抽样时间
$ t_3 $: 单次统计量计算时间
$ t_4 $: 结果输出时间

7.1 分层抽样

分层抽样是降低蒙特卡洛模拟方差的一种方法，核心是“把抽样区间分成多个‘层’，在每层内单独抽样、计算，最后合并结果”。

比如用蒙特卡洛法估算$\pi$：原本是在$[-1,1]$的正方形里随机投点，数落在圆内的点占比（$\pi\approx4\times\text{圆内点数/总点数}$）。

分层抽样的操作是：

分层：把正方形的$x$区间（$[-1,1]$）分成$m$个小层（比如分成100个小区间）；
每层单独抽样：在每个小层里都投一些点，计算该层内“圆内点数的占比”；
合并结果：把每层的结果按“层的占比”加权平均，得到最终的$\pi$估计值。

分层抽样的本质是把“波动大的区域”拆分成多个“波动小的子区域”，在每个子区域内抽样，能减小每个子区域内的结果波动；最终合并的结果，整体方差会比“直接在大区域里随机抽样”小很多

7.1.1 例一

用蒙特卡洛法估算$\pi$：

正方形（边长2，面积4）里画一个圆（半径1，面积$\pi$）；
随机投点，圆内点数占总点数的比例≈$\pi/4$，所以$\pi≈4×\text{圆内点数/总点数}$。

对比两种方法：

直接模拟：随便投点，结果波动大（比如10³次抽样，$\hat{\pi}_1=3.1760$，离真实值3.14159…差得远）；
分层抽样：把区间分成小层再投点，结果精度高（10³次抽样，$\hat{\pi}_2$就接近真实值）。

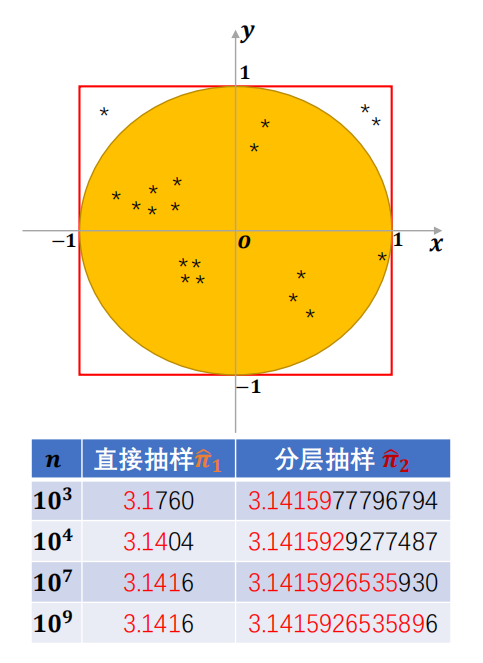
把$x$的区间$[-1,1]$分成$m$个小层（比如分成100层），第$k$层的范围是$\left[\frac{k-1}{m},\frac{k}{m}\right]$（这里$m$是层数）。

公式里的$X^k = \frac{1}{m}(U + (k-1))$是在第$k$层里生成随机数：

$U$是(0,1)的均匀随机数；
代入后，$X^k$会落在第$k$层的区间里（比如$k=1$、$m=100$，$X^1$落在$[0,0.01]$）。

对第$k$层，生成$n_k$个随机点（$n_k$是第$k$层的抽样次数），用$h_k(X^k)$判断点是否在圆内（在圆内是1，否则是0）。

公式里的$\frac{1}{n_k}\sum_{i=1}^{n_k} h_k(X^k_i)$是第$k$层内的圆内点比例（比如第$k$层投了10个点，6个在圆内，比例就是0.6）。

把每层的“圆内点比例”按“层的占比”加权平均，再乘以4得到$\pi$的估计值。

公式$\hat{\pi}2 = \frac{4}{m}\sum{k=1}^{m} \frac{1}{n_k}\sum_{i=1}^{n_k} h_k(X^k_i)$的意思是：

$\frac{1}{m}$是“每层的占比”（因为分成了$m$层，每层占1/m）；
先算每层的“圆内点比例”，再用$\frac{1}{m}$加权求和，最后乘以4，就是$\pi$的估计值。

7.1.2 分层抽样的数学逻辑

将长度$L$的区间分成$m$层(段)，$p_j$为第$j$层所占概率.随机变量$X_j$的概率分布为$f(x_j)$,则有统计量$h_j(x)$取值$h(x_j)$: $p_j = \int_{Z_j} f(x)dx,\sum_{j=1}^m p_j = 1.$ 这里第$j$层随机变量概率分布$f(x_j) = p_j^{-1}f(x).$

第$j$层统计量的期望 $\mu_j = E(h_j) = \int_{x_{j,\min}}^{x_{j,\max}} h(x_j)f(x_j)dx_j$
第$j$层分层抽样技巧统计量期望 $\mu = E[h] = \sum_{j=1}^m p_jE[h(X_j)]$
相应统计量估计值分别为 $\hat{h}_j = \frac{1}{n_j}\sum_{i=1}^{n_j} h(X_i^j),\quad \hat{h} = \sum_{j=1}^m p_j\hat{h}(X_i)$
相应统计量估计值的方差分别为 $Var(\hat{h}_j) = \frac{1}{p_j}\int_{x_{j,\min}}^{x_{j,\max}} (h(x_j) - E[h_j])^2 f(x_j)dx_j$

\[Var(\hat{h}) = \sum_{j=1}^m p_j^2Var(\hat{h}_j)/n_j\]

总样本数 $n = \sum_{j=1}^m n_j$

7.1.3 如何分配每层的抽样次数$n_j$

想要让分层抽样的结果波动（方差）最小, 这里给出两种方式

（1）比例分层抽样技巧

第$j$层样本数：$ n_j = np_j,j = 1,\cdots,m $
统计量估计值： $\hat{h}^* = \frac{1}{n} \sum_{j=1}^{m} \sum_{i=1}^{n_j} h\left( x_j^{(i)} \right)$
记整层抽样估计方差为 $\text{Var}(\hat{h}) = \int h^2(x)f(x)dx - \left( E[h(X)] \right)^2$
可以证明： $\text{Var}(\hat{h}^*) \leq \text{Var}(\hat{h})$ 这种方式的方差已经比直接抽样小

（2）最优分层抽样技巧

令 $\text{Var}(h) = \sum_{j=1}^{m} p_j^2\text{Var}(h_j)/n_j \stackrel{def}{=} \sum_{j=1}^{m} p_j^2\sigma_j^2/n_j$ 取极小的$n_j$，即获得最小方差，此时 $n_j = np_j\sigma_j / \sum_{j=1}^{m} p_j\sigma_j,j = 1,2,\cdots,m$
最优分层统计量估计值的方差为： $\text{Var}[h(n_1,n_2,\cdots,n_m)] = \frac{1}{n}\left( \sum_{j=1}^{m} p_j\sigma_j \right)^2$

7.2 重要性抽样

顾名思义：只改变概率分布，起源于变量代换方法。记$X$为随机变量, $f(x)$是它的概率分布, $h(x)$表示统计量，则重要抽样可得到重要概率密度分布$g(x)$, 其权重为： $\omega(x) = \frac{f(x)}{g(x)} < 1$

则模拟$n$次的统计量无偏估计为 $\hat{h} = \frac{1}{n} \sum_{i=1}^{n} h(X_i)\omega(X_i)$

其数学期望也为$\mu$。容易计算, 其方差为 $\text{Var}_g(h) = \int h^2(x)\omega^2(x)g(x)dx - \mu^2,$

与直接模拟得到的统计量方差区别(右端为负): $\text{Var}_g(h) - \text{Var}_f(h) = \int h^2(x)\left(\omega(x) - 1\right)f(x)dx.$

7.3 控制变量法

步骤1：构造变换后的统计量

对原统计量 $ h(x) $ 做不改变分布的变换，引入控制变量 $ h_1(x) $ 和任意常数 $ \alpha $，构造新统计量： $h^*(x) = h(x) + \alpha \left( E[h_1] - h_1(x) \right)$

对应的估计值为（基于 $ n $ 个样本 $ X_i $）： $\hat{h}^* = \frac{1}{n} \sum_{i=1}^n h^*(X_i)$

步骤2：计算变换后统计量的方差

对 $ h^*(x) $ 求方差，利用方差的运算性质（$ \text{Var}(aX+bY)=a^2\text{Var}(X)+b^2\text{Var}(Y)+2ab\text{Cov}(X,Y) $），展开得： $\text{Var}(h^*) = \text{Var}(h) + \alpha^2 \text{Var}(h_1) - 2\alpha \cdot \text{Cov}(h, h_1)$

步骤3：求最优参数 $ \alpha^* $

为了最小化 $ \text{Var}(h^*) $，对 $ \alpha $ 求导并令导数为0，得到 $ \alpha $ 的最优值： $\alpha^* = \frac{\text{Cov}(h, h_1)}{\text{Var}(h_1)} = \text{Corr}(h, h_1) \sqrt{\frac{\text{Var}(h)}{\text{Var}(h_1)}}$

将 $ \alpha^* $ 代入方差公式，得到最小方差： $\text{Var}(h^*) = \text{Var}(h) - \frac{\left( \text{Cov}(h, h_1) \right)^2}{\text{Var}(h_1)} = \left( 1 - \left( \text{Corr}(h, h_1) \right)^2 \right) \cdot \text{Var}(h)$

步骤4：方差缩减的效果

最终，变换后统计量的方差与原统计量方差的比值为： $\frac{\text{Var}(h^*)}{\text{Var}(h)} = 1 - \left( \text{Corr}(h, h_1) \right)^2$

（注：若 $ h $ 是积分 $ \int f(x)dx $，可以构造与 $ f $ 接近的可积函数 $ g(x) $，通过 $ \int f(x)dx = \int (f(x)-g(x))dx + \int g(x)dx $ 缩减方差——因为 $ (f(x)-g(x)) $ 的波动比 $ f(x) $ 小）

7.4 对偶随机变量

步骤1：核心思想与统计量构造

不改变随机变量的概率分布，只调整统计量：构造对偶随机变量对应的统计量 $ h^*(x) $，形式为两个负相关统计量的均值： $h^*(x) = \frac{1}{2}\left( h_1(x) + h_2(x) \right)$ 其中 $ h_1(x) $ 和 $ h_2(x) $ 是负相关的（负相关性越强，方差缩减效果越好）。

步骤2：基于均匀分布的具体计算（$ X \sim U(0,1) $）

若随机变量 $ X $ 服从区间 $ (0,1) $ 上的均匀分布（即 $ X \sim U(0,1) $）：

取 $ h_1(x) = h_1(U) $（$ U $ 是均匀分布的随机数），
取其对偶统计量 $ h_2(x) = h_2(1-U) $（用 $ 1-U $ 替换 $ U $）。

此时，对偶统计量为： $h^*(X) = \frac{1}{2}\left( h_1(U) + h_2(1-U) \right)$

抽样 $ n $ 次后，统计量的估计值为： $\hat{h}^* = \frac{1}{2n} \sum_{i=1}^n \left( h_1(U_i) + h_2(1-U_i) \right)$

步骤3：基于正态分布的扩展（$ X \sim N(\mu, \sigma^2) $）

若随机变量 $ X $ 服从正态分布（即 $ X \sim N(\mu, \sigma^2) $）：

取 $ h_1(x) = h_1(X) $，
取其对偶统计量 $ h_2(x) = h_2(2\mu - X) $（用 $ 2\mu - X $ 替换 $ X $，利用正态分布的对称性）。

此时，统计量的估计值为： $\hat{h}^* = \frac{1}{2n} \sum_{i=1}^n \left( h_1(X_i) + h_2(2\mu - X_i) \right)$

为什么对偶随机变量减小方差

对偶随机数能减小方差的核心原因是：构造的两个统计量是“负相关”的，负相关会抵消波动，从而降低整体方差。

对偶统计量是 $ h^* = \frac{1}{2}(h_1 + h_2) $，其方差为： $\text{Var}(h^*) = \frac{1}{4}\left[ \text{Var}(h_1) + \text{Var}(h_2) + 2\text{Cov}(h_1, h_2) \right]$

对偶随机数的关键是让 $ h_1 $ 和 $ h_2 $ 负相关（即 $ \text{Cov}(h_1, h_2) < 0 $）。

若 $ h_1 $ 和 $ h_2 $ 是“对称”的（比如均匀分布中 $ h_2=h_1(1-U) $、正态分布中 $ h_2=h_1(2\mu-X) $），通常满足 $ \text{Var}(h_1) = \text{Var}(h_2) $，代入方差公式得： $\text{Var}(h^*) = \frac{1}{2}\left[ \text{Var}(h_1) + \text{Cov}(h_1, h_2) \right]$
因为 $ \text{Cov}(h_1, h_2) < 0 $，所以 $ \text{Var}(h^*) < \frac{1}{2}\text{Var}(h_1) $，而原统计量 $ h_1 $ 的方差是 $ \text{Var}(h_1) $——显然对偶统计量的方差被缩小了。

负相关性越强（$ \text{Cov}(h_1, h_2) $ 越负），方差缩减的幅度就越大。

7.5 公共随机数

公共随机数的核心是让两个统计量共享同一组随机数，从而利用它们的相关性缩减方差，推导过程如下：

构造统计量 我们需要估计的是两个统计量的差值 $ h(X) = h_1(X) - h_2(X) $，其期望为： $E[h] = E[h_1] - E[h_2]$
对比两种模拟方法的方差
- 直接模拟（不共享随机数）：若 $ h_1 $ 和 $ h_2 $ 用独立的随机数模拟，两者是独立的（协方差 $ \text{Cov}(h_1,h_2)=0 $），此时方差为： $\text{Var}(h_1) + \text{Var}(h_2)$
- 公共随机数（共享随机数）：若 $ h_1 $ 和 $ h_2 $ 用同一组随机数模拟，两者会产生正相关性（$ \text{Cov}(h_1,h_2) > 0 $），此时差值的方差为： $\text{Var}(h_1 - h_2) = \text{Var}(h_1) + \text{Var}(h_2) - 2\text{Cov}(h_1,h_2)$

公共随机数减小方差的原因, 关键在于 “正相关性”抵消了波动：当 $ h_1 $ 和 $ h_2 $ 正相关（$ \text{Cov}(h_1,h_2) > 0 $）时，公式中的 $ -2\text{Cov}(h_1,h_2) $ 会让方差变小，即： $\text{Var}(h_1 - h_2) < \text{Var}(h_1) + \text{Var}(h_2)$

7.6 条件期望

这里用到的是方差分解公式（全方差公式），推导基于期望和方差的定义：

对于两个随机变量 $ X $ 和 $ Z $，方差分解公式为： $\text{Var}(X) = \text{Var}\left( E[X|Z] \right) + E\left[ \text{Var}(X|Z) \right]$

推导过程（核心步骤）：

先将 $ X $ 拆分为“条件期望 + 残差”： $X = E[X|Z] + \left( X - E[X|Z] \right)$

对两边求方差（利用“条件期望的期望等于原期望” $ E[E[X	Z]] = E[X] $，以及残差的期望 $ E[X - E[X	Z]] = 0 $）：
交叉项的协方差 $ \text{Cov}\left( E[X	Z], X - E[X	Z] \right) = 0 $，因此方差可分解为两项之和，即得到全方差公式。

条件期望减小方差的原因

从全方差公式可以直接得出：由于方差始终非负（$ E\left[ \text{Var}(X|Z) \right] \geq 0 $），因此： $\text{Var}(X) \geq \text{Var}\left( E[X|Z] \right)$

这说明：**用“条件期望 $ E[X

Z] $ 的样本均值”估计 $ X $，其方差会小于（或等于）直接用 $ X $ 样本均值的方差**。

条件期望技巧的算法流程

通过引入关联随机变量 $ Z $，步骤是：

从 $ Z $ 的分布 $ g(z) $ 中抽样得到 $ Z_1, Z_2, …, Z_n $；
对每个 $ Z_i $，解析计算条件期望 $ E[X Z_i] $；
用这些条件期望的均值作为 $ X $ 的估计： $\hat{X} = \frac{1}{n}\sum_{i=1}^n E[X|Z_i]$

7.7 样本分裂

这个方法是样本分裂与轮盘赌技巧（属于蒙特卡罗模拟中的方差缩减技术），核心是通过“重点区域多采样、非重点区域控制采样”来降低方差，推导和方差缩减的逻辑如下：

样本分裂的推导逻辑

首先将模拟区域 $ A $ 划分为 重要区域 $ S $（对结果贡献大、需要更精确估计）和 不重要区域 $ R $（对结果贡献小、可简化采样），针对不同区域设计不同的采样策略：

1. 重要区域 $ S $：样本分裂

当粒子在重要区域 $ S $ 运动时，每过一层就将1个粒子分裂为 $ v $ 个粒子：

每个分裂后的粒子能量、方向与原粒子一致；
每个粒子的“权重”变为 $ 1/v $（保证总贡献不变）；
记录这 $ v $ 个粒子的贡献 $ I_k $（$ k=1,2,…,v $）。

2. 不重要区域 $ R $：轮盘赌压缩

当粒子在不重要区域 $ R $ 运动时，将 $ v $ 个粒子压缩为1个，并用轮盘赌决定是否继续跟踪：

压缩后的粒子权重变为 $ v $；
以概率 $ q=1/v $ 继续跟踪该粒子（记录其贡献 $ I_1/q $，补全权重）；
以概率 $ 1-q $ 终止该粒子的模拟。

3. 总贡献的表达式

第 $ i $ 次模拟、第 $ j $ 次碰撞的总贡献 $ I_{ij} $，是“重要区域分裂贡献”和“不重要区域轮盘赌贡献”的和（$ \eta(\cdot) $ 是指示函数，满足条件时取1，否则取0）： $I_{ij} = \frac{1}{v}\sum_{k=2}^v I_k \cdot \eta(A \in S) + \frac{I_1}{q} \cdot \eta(A \in R, U \leq q)$

最终，$ n $ 次模拟、每次 $ m $ 次碰撞的总贡献估计为： $\hat{I} = \frac{1}{n}\sum_{i=1}^n \sum_{j=0}^m I_{ij}$

样本分裂能减小方差的原因

核心是 “在重要区域增加采样数量，提高估计精度”：

重要区域 $ S $ 对结果的影响大，若采样太少，随机波动会导致方差大；通过“分裂粒子”，相当于在重要区域增加了有效样本量，能更精确地估计该区域的贡献，从而降低整体方差。
不重要区域 $ R $ 对结果的影响小，即使减少采样（通过轮盘赌压缩），对整体结果的波动影响也很小；同时压缩样本还能降低计算成本。

7.8 序贯抽样(Sequential Monte Carlo, SMC)

这个图展示的是贯序抽样（序贯抽样）的模拟计算流程，核心是通过“逐步抽样+条件分布+统计量估计”来模拟随机过程，下面分两部分拆解：

贯序抽样的数学基础

贯序随机变量（随机过程） 贯序抽样的对象是一个按顺序生成的随机变量序列 $ X = {X_1, X_2, \dots, X_m} $，不是一次性抽取的固定样本，而是“逐个产生”的随机过程。
联合概率分布的表示 因为序列是“后一个变量依赖前一个”的，所以整个序列的联合概率分布可以拆成条件概率的乘积： $f(x) = f(x_1)f(x_2|x_{1:1})f(x_3|x_{1:2})\dots f(x_m|x_{1:m-1}) = \prod_{k=1}^m f(x_k|x_{1:k-1})$ （注：$ x_{1:k-1} $ 表示前 $ k-1 $ 个样本的观测值，$ f(x_1|x_{1:0}) $ 是初始分布，即第一个样本的概率分布）

贯序抽样的模拟过程

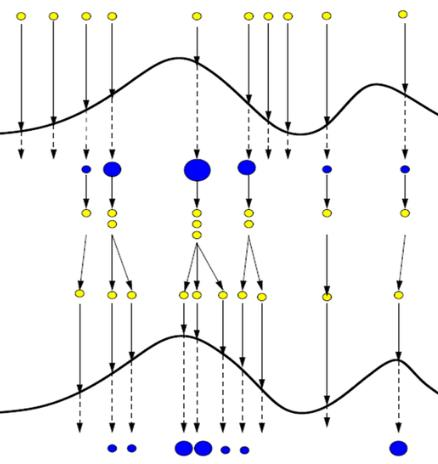
这个流程是用“多次迭代+多次抽样”来模拟贯序抽样的结果，具体步骤：

外层循环（$ k=1,2,\dots,m $）：模拟第 $ k $ 个样本的生成

内层循环（$ i=1,2,\dots,n $）：对第 $ k $ 个样本做 $ n $ 次重复抽样（减少误差）

抽样：从“依赖前 $ k-1 $ 个样本的条件分布” $ f(x_k

x^i_{1:k-1}) $ 中，抽取第 $ i $ 次重复下的第 $ k $ 个样本 $ X^i_k $；

计算统计量：对抽到的 $ X^i_k $，计算我们关心的统计量 $ h(X^i_k) $（比如均值、方差等）；

内层循环结束后：估计第 $ k $ 个样本的统计量

用 $ n $ 次重复抽样的结果，求统计量的均值，作为第 $ k $ 个样本的统计量估计值： $\hat{h}_k = \frac{1}{n}\sum_{i=1}^n h(X^i_k)$

外层循环结束后：评估模拟精度

计算均方根误差（RMSE），衡量模拟结果与真实值的偏差： $RMSE = \left( \frac{1}{m}\sum_{k=1}^m (\hat{h}_k - h_k)^2 \right)^{\frac{1}{2}}$ （其中 $ h_k $ 是第 $ k $ 个样本统计量的真实值）

贯序重要性抽样

序贯抽样中，目标分布 $ f(x) $（比如系统真实状态的分布）可能很难直接抽样，因此SIS选择一个容易抽样的“重要性分布” $ g(x) $，用 $ g(x) $ 抽样本，再给每个样本分配“权重”来修正偏差。

样本权重的定义 第 $ k $ 次迭代的样本权重 $ \omega(x_k) $，是目标分布 $ f(x) $ 与重要性分布 $ g(x) $ 的比值： $\omega(x_k) = \frac{f(x)}{g(x)} = \frac{\prod_{k=1}^m f(x_k|x_{1:k-1})}{\prod_{k=1}^m g(x_k|x_{1:k-1})}$ （这里 $ f(x_k|x_{1:k-1}) $ 是序贯抽样的条件分布，$ g(x_k|x_{1:k-1}) $ 是重要性分布的条件分布）
权重的递推关系（序贯的核心） 因为是“序贯”过程，权重可以利用前一步的结果递推计算，不用每次重新计算所有样本： $\omega(x_k) = \omega(x_{k-1}) \cdot \frac{f(x_k|x_{1:k-1})}{g(x_k|x_{1:k-1})}$
- 初始权重：第1个样本的权重 $ \omega(x_1) = \frac{f(x_1)}{g(x_1)} $
- 后续权重：每一步都用“前一步权重 × 当前步的条件分布比值”更新
统计量的估计 最终用“加权平均”来估计目标统计量 $ h(X) $（比如系统状态的均值）： $\hat{h}_k = \frac{1}{n}\sum_{i=1}^n h(X^i_k) \cdot \omega(X^i_k)$ （$ n $ 是样本数，$ X^i_k $ 是第 $ i $ 个样本在第 $ k $ 步的取值）

样本退化问题

样本退化问题是序贯重要性抽样（SIS）中特有的缺陷：随着迭代次数增加，大部分样本的权重会变得极小，只有极少数样本拥有几乎全部权重，导致样本失去对目标分布的代表性。

核心原因是权重的递推放大了方差。SIS的权重是递推计算的：$ \omega(x_k) = \omega(x_{k-1}) \cdot \frac{f(x_k|x_{1:k-1})}{g(x_k|x_{1:k-1})} $。每次迭代，权重会乘以“目标条件分布与重要性条件分布的比值”——若这个比值在多数情况下小于1，权重的方差会快速增大：少数样本的权重持续累积（越来越大），而大部分样本的权重持续缩小（趋近于0）。

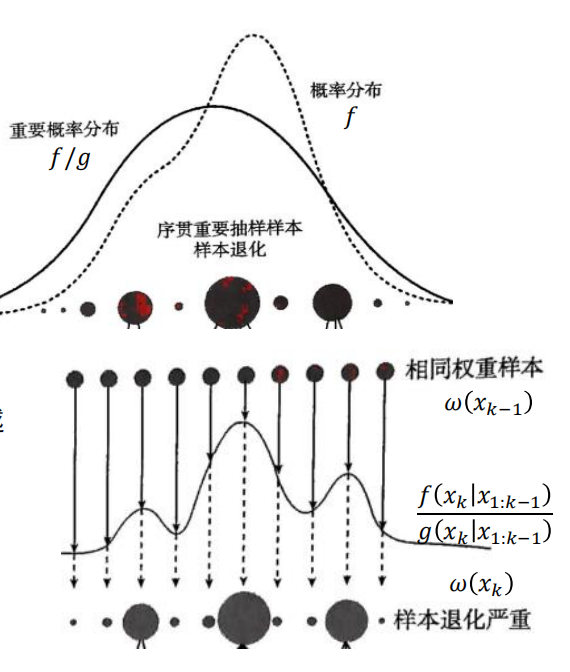
初始阶段：样本权重差异不大（图中“相同权重样本”）；
迭代后：只有极少数样本的权重很大（图中深色大圆点），绝大多数样本权重趋近于0（图中小圆点）；
最终结果：这些“权重趋近于0的样本”对估计几乎没有贡献，相当于“无效样本”，样本整体失去了对目标分布的覆盖能力。

样本退化会让SIS的估计精度急剧下降，甚至失去意义——这也是1950s-1990s期间，序列蒙特卡洛（SMC）方法发展缓慢的核心原因。Doucet等人（2001）证明：样本退化是SIS的必然现象（只要重要性分布与目标分布不完全一致，权重方差就会随迭代增大）。

解决方法通常是重采样（比如粒子滤波中的重采样步骤）：剔除权重极小的样本，复制权重极大的样本，让样本重新拥有合理的权重分布。

样本分裂与重采样

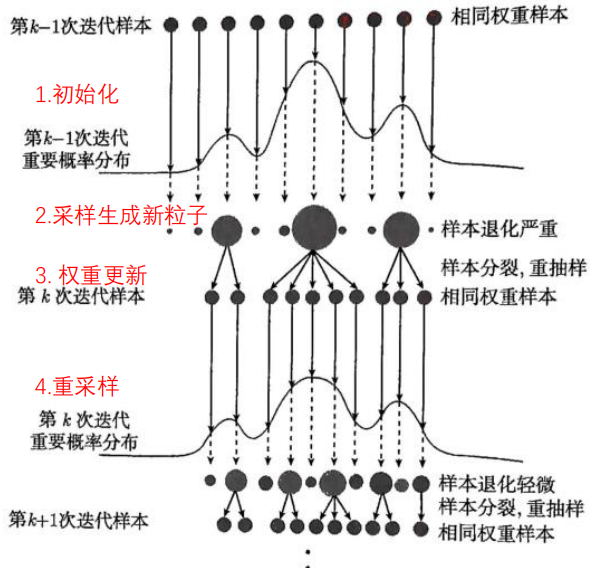
样本分裂和重采样是解决序贯重要性抽样（SIS）中“样本退化”的两种核心方法，同时也会带来新的“样本贫化”问题。

样本分裂把“权重大的样本”拆分成多个“权重相同的小样本”，让权重分布更均匀，抑制样本退化。

操作：比如一个样本的权重是5，就把它分裂成5个权重为1的小样本；
作用：避免少数样本独占高权重，让更多样本参与后续估计，维持样本对目标分布的代表性（对应图中“权重大的样本分裂成多个小样本”）。

重采样通过“淘汰小权重样本+复制大权重样本”，重置样本的权重分布，解决样本退化。具体步骤：

权重归一化：先把所有样本的权重换算成“相对占比”（$ \widetilde{\omega}(X_k^i) = \frac{\omega(X_k^i)}{\sum_{l=1}^n \omega(X_k^l)} $），确保权重和为1；
淘汰与复制：按归一化后的权重概率，淘汰权重极小的样本，复制权重极大的样本（比如权重占比80%的样本，会被复制多次）；
重置权重：重采样后的样本权重统一设为相等值（比如都设为1），让样本重新拥有均匀的权重分布。

不过，重采样也有副作用——淘汰过多小权重样本，导致样本失去多样性：

比如所有小权重样本都被淘汰，只剩下少数大权重样本的复制品，样本会集中在目标分布的局部区域，无法覆盖整个分布的特征（相当于“样本多样性被剥夺”）。

8 马尔科夫链蒙特卡罗(MCMC)

8.1 简单蒙特卡洛(MC)方法的局限性

抽样效率: 指 “用较少的样本量就能得到可靠结果” 的能力。效率越高，越能以低成本（时间 / 计算资源）完成估计；效率低则需要极多样本，甚至无法完成计算。

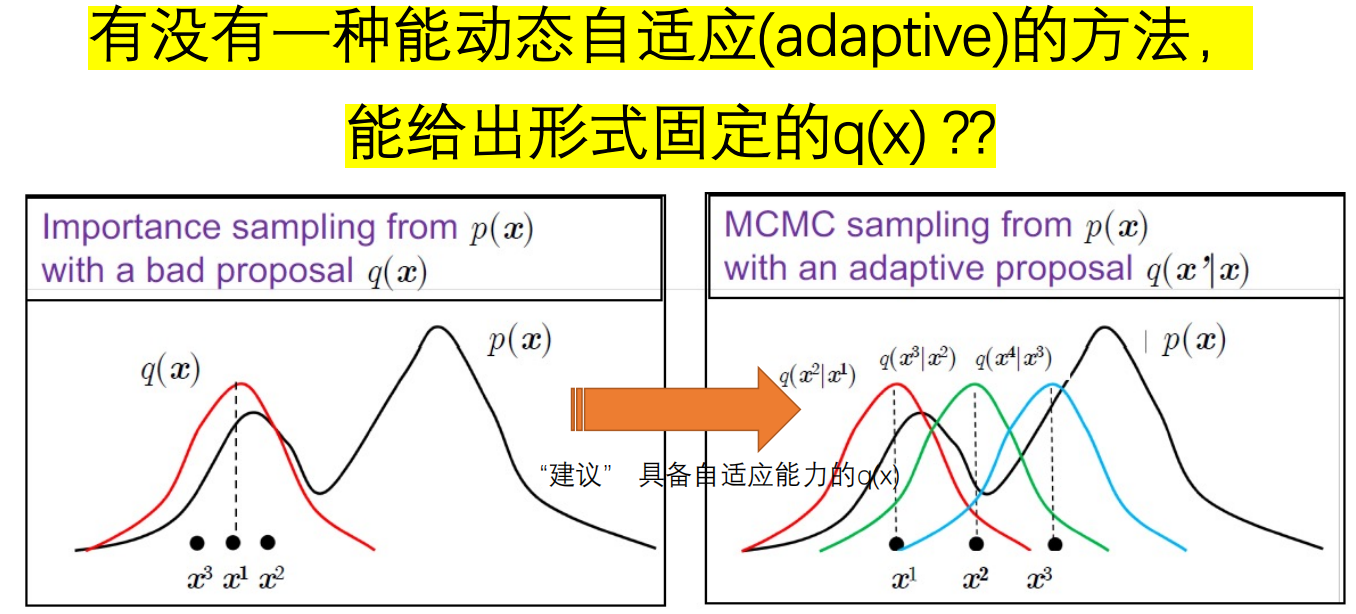
提议分布设计: 在重要性抽样、拒绝 - 接受抽样中，需要先构造一个容易抽样的分布 q(x) 即 “提议分布”，再基于 q(x) 生成样本并修正，以逼近目标分布 p(x) 。

简单 MC 的局限集中在抽样效率和提议分布上：

直接抽样效率低：面对高维问题或稀有事件时，有效样本占比太少，需要极多样本才能得到可靠结果；
提议分布相关缺陷：若提议分布 q(x) 与真实分布 p(x) 差异大，拒绝 - 接受 / 重要性抽样的效率会很低；构造 “匹配 p(x) 的好 q(x)” 本身很困难（因为实际中 p(x) 往往复杂未知）

8.2 随机过程

随机过程是随机变量的集合，记为${X_t, t \in T}$。

其中：

$T$是“指标集”，可以是离散的（比如$T={1,2,3,…}$，对应“随机变量序列”），也可以是连续的（比如$T=[0,+\infty)$）；
每个$X_t$是一个随机变量，整个集合描述了“随指标（通常是时间）变化的随机现象”。

常见的随机过程包括Poisson过程、Markov过程等。

8.2.1 Poisson过程

Poisson过程是描述“事件在时间轴上随机发生次数”的随机过程.

假设事件在$[0, t]$上任意时刻发生, $N(t)$表示$[0,t]$内事件发生的次数. 核心是满足3个条件的计数过程$N(t)$：

初始条件：$N(0)=0$（初始时刻事件发生次数为0）；
独立增量：任意不重叠的时间区间内，事件发生的次数相互独立（比如$[0,t_1]$和$[t_1,t_2]$内的发生次数无关）；
增量服从Poisson分布：对任意时间间隔$t>0$，任意起始时刻$s≥0$，区间$[s,s+t]$内事件发生$k$次的概率满足： $P\{N(s+t)-N(s)=k\} = \frac{(\lambda t)^k e^{-\lambda t}}{k!}$ 其中$\lambda>0$是“速率”（表示单位时间内事件发生的平均次数）。

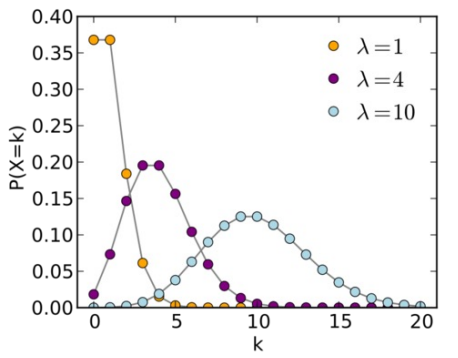
可以注意到，泊松分布是一个递增函数乘以递减函数。$\lambda$越大，峰值越向后偏移。

简单说，Poisson过程是 用来刻画随机、独立发生的事件的计数规律 的模型（比如某路口单位时间内的车流量、客服中心的呼叫次数等）。

8.2.2 Markov过程

Markov过程是满足“无后效性”的随机过程，核心特点是“未来的状态只依赖于当前状态，与过去的状态无关”。

对于随机过程$ X = {X_t, t \in R} $，若满足： $P(X_{t+1} = x_{t+1} | X_0 = x_0, \dots, X_t = x_t) = P(X_{t+1} = x_{t+1} | X_t = x_t)$ 简单说：已知“现在”，“未来”的概率分布与“过去”无关，这一性质叫“Markov性”（无后效性）。

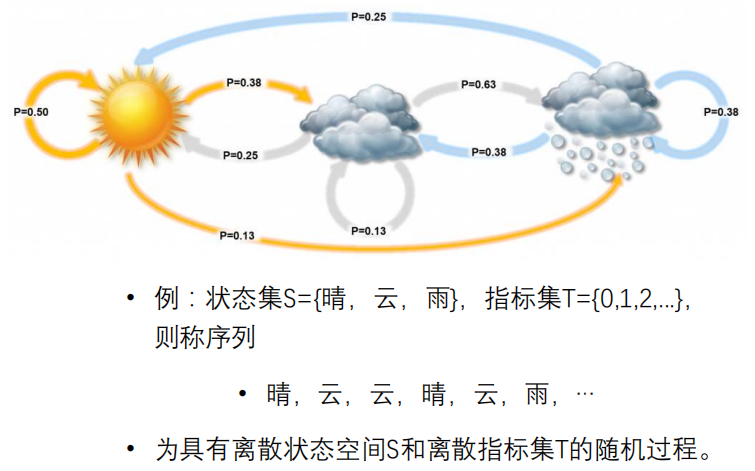
状态可以是离散的（比如“晴、云、雨”），也可以是连续的；
指标集（通常是时间）可以是离散的（比如“每天的状态”）或连续的。

举个例子, 比如：

青蛙在荷花池的跳跃（下一个位置只和当前位置有关）；
天气变化（明天的天气只依赖今天的天气，和昨天无关）；
传染病受感染的人数
原子核中一自由电子的跳跃
人口增长过程
股价波动、布朗运动等。

8.2.3 Markov Chain 马尔科夫链

马尔可夫链（Markov Chain）是“离散时间下满足马尔可夫性的随机过程”. 是按时间顺序排列的一系列状态序列：$ x^{(0)}, x^{(1)}, x^{(2)}, \dots, x^{(n)}, x^{(n+1)}, \dots $，描述状态之间“前后相继”的转换过程。

连续时间Markov过程 考虑随机过程 $ X = {X_t, t \in R} $，满足： $P(X_{t+1} = x_{t+1} \mid X_0 = x_0, \dots, X_t = x_t) = P(X_{t+1} = x_{t+1} \mid X_t = x_t)$

离散时间马尔可夫链

描述了从状态 $ x_i $ 到状态 $ x_j $ 的转换的随机过程。
假设存在一个独立于时间的固定概率 $ p_{ij} $，使得： $P(x^{(n+1)} = i \mid x^{(n)} = j, x^{(n-1)} = i_{n-1}, \dots, x^{(0)} = i_0) = p_{ij}, n \geq 0.$

马尔科夫性(无记忆性): 下一个状态的概率只由当前状态决定，与过去的所有状态无关： $P(x^{(n+1)} = i \mid x^{(n)} = j, x^{(n-1)} = i_{n-1}, \dots, x^{(0)} = i_0) = p_{ij}$ 其中 $ p_{ij} $ 是固定的状态转移概率（与时间无关）。

8.2.4 转移概率矩阵

考虑一个特殊的情况, 在齐次马尔可夫链（状态转移概率与时间无关）中，定义概率 $ p_{ij} $ 为：

\[p_{ij} = P(X_{t+1} = j \mid X_t = i)\]

它表示“当前处于状态 $ i $ 时，下一个时刻转移到状态 $ j $ 的概率”。

非负性：$ p_{ij} \geq 0 $（概率不能为负）；
归一性：$ \sum_{j=0}^{\infty} p_{ij} = 1 $（从状态 $ i $ 转移到所有可能状态的概率之和为1）。

将所有状态的转移概率 $ p_{ij} $ 按“行（当前状态）、列（下一状态）”排列，组成的矩阵： $P = \begin{pmatrix} p_{00} & p_{01} & \dots \\ p_{10} & p_{11} & \dots \\ \vdots & \vdots & \vdots \end{pmatrix}$ 这个矩阵就叫 （一步）转移概率矩阵 ，它完整描述了马尔可夫链中“状态之间的转移规律”——是转移概率的“模型化表达”。

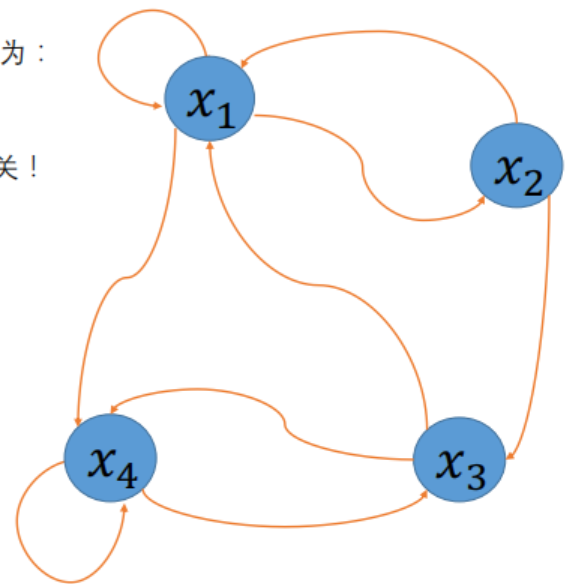
简单说：转移概率矩阵（转移概率模型）是用矩阵形式，统一记录马尔可夫链中所有状态间的转移概率，从而量化状态转移的规律。

8.2.5 平稳分布

平稳分布是马尔可夫链在长期运行后状态概率不再变化的稳定分布

如果一个非周期的Markov链有状态转移矩阵$ P $，并且它的任意两个状态是连通的，那么： $\lim_{n \to \infty} P_{ij}^n = \pi(j) = \sum_{i=1}^{\infty} \pi_i P_{ij}$ 存在且与$ i $无关，即 $\lim_{n \to \infty} P^n = \begin{pmatrix} \pi(1) & \pi(2) & \dots & \pi(j) & \dots \\ \pi(1) & \pi(2) & \dots & \pi(j) & \dots \\ & & \dots & & \\ \pi(1) & \pi(2) & \dots & \pi(j) & \dots \\ & & \dots & & \end{pmatrix}$

其中，状态概率分布 $ \pi(j) = \sum_{i=1}^{\infty} \pi_i P_{ij} $。此外：

$ \pi $是方程$ \pi P = \pi $的唯一非负解；
$ \pi = [\pi(1), \pi(2), \dots, \pi(j), \dots] $满足$ \sum_{i=1}^{\infty} \pi_i = 1 $。

此时，我们称$ \pi $是这个Markov链的平稳分布。

直观来说：当马尔可夫链的状态概率分布达到 $ \pi $ 后，再经过一次转移，概率分布依然是 $ \pi $（状态概率不再随时间变化）。

Perron-Frobenius 定理

如果概率转移矩阵$ P $满足： $p_{i,j} > \delta > 0,\ \forall\ i,j$

即从任意状态 $i$ 转移到任意状态 $j$ ，都有至少 $δ$ 的概率. 那么，有以下结论：

1. $ P $存在特征值为1的唯一左特征向量$ \vec{w} $, 即满足 $\vec{w} P = 1 \cdot \vec{w}$，且$ \vec{w} $的所有分量严格为正； 2. 若将此特征向量归一化（即满足$ \sum w_i = 1 $），则： $\lim_{n \to \infty} P^n = \vec{1}\vec{w}$ （其中$ \vec{1} $是全1列向量，$ \vec{1}\vec{w} $表示每一行均为$ \vec{w} $的矩阵）

也就是说, 无论初始状态是什么，经过足够多步转移后，系统处于各状态的概率都会收敛到$ \vec{w} $（即平稳分布）。

细致平稳条件/定理

细致平稳条件的核心等式为： $\pi_i p_{i,j} = \pi_j p_{j,i} \tag{1}$

即 “从状态$i$到$j$的概率流” 等于 “从$j$到$i$的概率流”，则称$π$和$P$满足细致平稳条件。

只要满足细致平稳条件，就能直接推导出平稳分布的核心要求. 要验证转移矩阵$ P $达到平稳分布$ \pi $，需满足平稳分布的核心方程：

\[\pi_j = \sum_{i=1}^{\infty} \pi_i p_{i,j} \tag{2}\]

利用细致平稳条件（1），可推导方程（2）成立： $\sum_{i=1}^{\infty} \pi_i p_{i,j} = \sum_{i=1}^{\infty} \pi_j p_{j,i} = \pi_j \sum_{i=1}^{\infty} p_{j,i} = \pi_j$ （注：$ \sum_{i=1}^{\infty} p_{j,i} = 1 $是转移矩阵的行和为1的性质）

至此，平稳分布的核心方程（2）得证。

所有的 MCMC（Markov Chain Monte Carlo）方法都是以这个定理作为理论基础的！

案例1

我们来看一个案例. 市场状态（牛、熊、平）构成的马尔可夫链，如何收敛到平稳分布

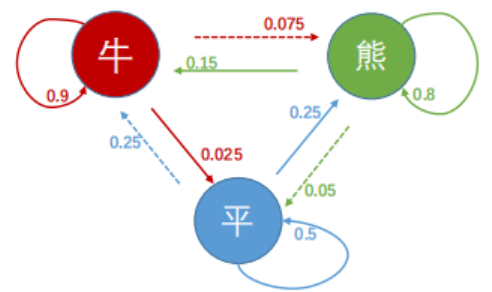
状态：3种市场状态——牛、熊、平；
转移矩阵 $ P $：描述状态间的转移概率（行是当前状态，列是下一状态）： $P = \begin{pmatrix} 0.9 & 0.075 & 0.025 \quad \text{（当前是“牛”，转牛/熊/平的概率）} \\ 0.15 & 0.8 & 0.05 \quad \text{（当前是“熊”，转牛/熊/平的概率）} \\ 0.25 & 0.25 & 0.5 \quad \text{（当前是“平”，转牛/熊/平的概率）} \end{pmatrix}$
初始状态分布 $ s $：初始时处于“牛、熊、平”的概率是 $ [0.12, 0.23, 0.65] $。

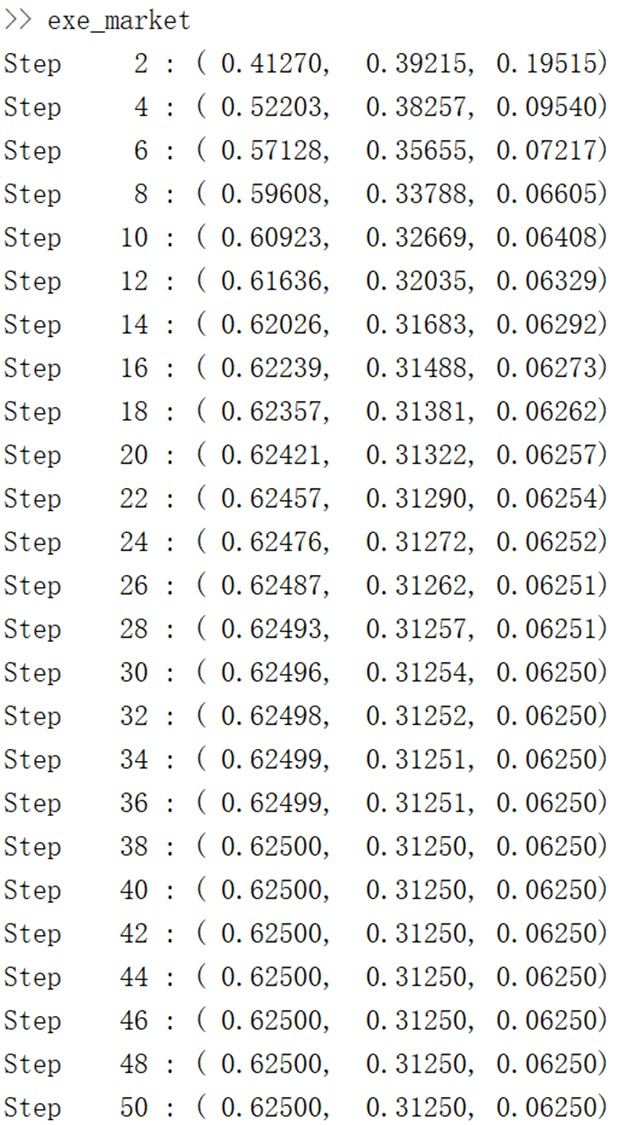
通过循环让初始分布 $ s $ 不断乘以转移矩阵 $ P $（模拟状态随时间的转移），可以看到：

初始几步（比如Step2），分布变化较大；
随着迭代次数增加（到Step40左右），分布逐渐稳定在 $ [0.62500, 0.31250, 0.06250] $；
之后无论再迭代多少次，分布都不再变化。

最终稳定的 $ [0.625, 0.3125, 0.0625] $ 就是这个马尔可夫链的平稳分布. 意味着“长期来看，市场处于‘牛’的概率是62.5%，‘熊’是31.25%，‘平’是6.25%”，且这个概率会保持稳定, 不再随时间变化。

案例2 : 周期性转移

状态：3个状态（1、2、3）；
转移概率矩阵 $ P $： $P = \begin{pmatrix} 0 & 1 & 0 \quad \text{（状态1只能转移到状态2）} \\ 0.5 & 0 & 0.5 \quad \text{（状态2以0.5概率转移到1或3）} \\ 0 & 1 & 0 \quad \text{（状态3只能转移到状态2）} \end{pmatrix}$
转移图规律：状态1→2→1/3→2→1/3…，呈现“2步一循环”的周期特征。

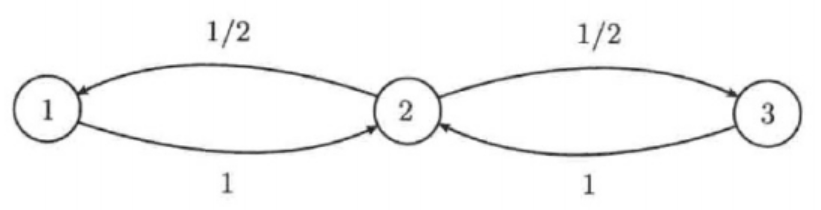
通过计算转移矩阵的幂可以验证：$ P^3 = P $（即3次转移等价于1次转移），说明该马尔可夫链的周期为2——从任意状态出发，回到原状态的步数必须是2的倍数（比如状态1→2→1，需要2步；状态3→2→3，也需要2步）。

尽管是周期链，它存在不变分布（不是平稳分布）：$ \pi = (0.25, 0.5, 0.25) $。

下面是计算不变分布的过程。不变分布 $\pi = (\pi_1, \pi_2, \pi_3)$ 需满足： $\pi P = \pi$ 同时满足概率归一化：$\pi_1 + \pi_2 + \pi_3 = 1$。

代入转移概率矩阵 $P$ 列方程，已知转移矩阵： $P = \begin{pmatrix} 0 & 1 & 0 \\ 0.5 & 0 & 0.5 \\ 0 & 1 & 0 \end{pmatrix}$

将 $\pi P = \pi$ 展开为分量形式：

第1个分量：$\pi_1 \cdot 0 + \pi_2 \cdot 0.5 + \pi_3 \cdot 0 = \pi_1$
第2个分量：$\pi_1 \cdot 1 + \pi_2 \cdot 0 + \pi_3 \cdot 1 = \pi_2$
第3个分量：$\pi_1 \cdot 0 + \pi_2 \cdot 0.5 + \pi_3 \cdot 0 = \pi_3$

从第1、3个分量的方程可得： $\pi_1 = 0.5 \pi_2, \quad \pi_3 = 0.5 \pi_2$

结合归一化条件 $\pi_1 + \pi_2 + \pi_3 = 1$，代入 $\pi_1、\pi_3$： $0.5 \pi_2 + \pi_2 + 0.5 \pi_2 = 1 \implies 2 \pi_2 = 1 \implies \pi_2 = 0.5$

进而得到： $\pi_1 = 0.5 \times 0.5 = 0.25, \quad \pi_3 = 0.5 \times 0.5 = 0.25$

该链的不变分布应为 $\pi = (0.25, 0.5, 0.25)$（严格满足 $\pi P = \pi$）。

注意, 周期链的不变分布是“长期平均的状态占比”，状态不会固定在某一分布，而是按周期波动, 长期均值稳定。

所有马尔可夫链都有状态转移矩阵， “非周期” 是平稳分布存在且唯一的必要条件之一. 周期的马尔可夫链，状态会陷入 “固定间隔的循环”，导致转移矩阵的幂 $P^{n}$ 没有稳定的极限，因此不存在平稳分布（或无法收敛到唯一的平稳分布）。

8.2.6 马尔科夫链的平稳性分析

实用马尔科夫链, 指能稳定应用（比如用于预测、建模）的马尔可夫链.

状态数有限（不能有无穷多状态）；
转移概率固定（状态之间的转换概率不随时间变）；
任意状态可互通（从任意一个状态，能通过若干步转到其他任意状态）；
无简单循环（不会陷入 “A→B→A” 这种死循环，无法收敛）。

8.3 马尔科夫链蒙特卡洛

MCMC抽样（马尔可夫链蒙特卡洛，Markov Chain Monte Carlo）是一种非常强大的统计方法，它的核心思想是：

当你无法直接从一个非常复杂的目标（比如一个形状极其古怪的山）上随机取样（比如随机空投抓人）时，MCMC提供了一种“间接”的取样方法。

它通过构造一个“智能”的随机游走过程（马尔可夫链），让这个游走过程最终在山上“待得久”的地方，恰好就是山峰（概率高）的地方。这样，你只需要记录下这个游走者的足迹，就相当于得到了你想要的样本。

蒙特卡洛是一种思想，指通过大量的随机抽样来估算一个（通常很难直接计算的）结果。例如投掷针估算圆周率. 但是蒙特卡洛方法的前提是你能做到“真正的随机抽样”（比如在正方形内均匀地扔石头）。但如果目标分布（比如那个湖的形状）非常复杂、维度非常高，你根本没法直接进行均匀抽样。这时就需要马尔可夫链登场了。

马尔科夫链是一个随机过程，它有一个关键特性，叫做“无记忆性”。过程中的下一个状态只取决于当前状态，而与“如何”到达当前状态的“历史路径”完全无关。而平稳分布说明, 只要这个“马尔可夫链”设计得当（满足某些条件，比如不可约性和对称性），无论它从什么状态开始，在它随机游走了足够长的时间后，它处于各个状态的概率会趋于一个稳定的分布。

我们的目标是想从一个特定的、复杂的概率分布 $P(x) $中抽样。我们的方法是设计一个马尔可夫链，当马尔可夫链运行足够久、达到平稳分布后, 链上的状态恰好就是我们想要的那个 $P(x)$.

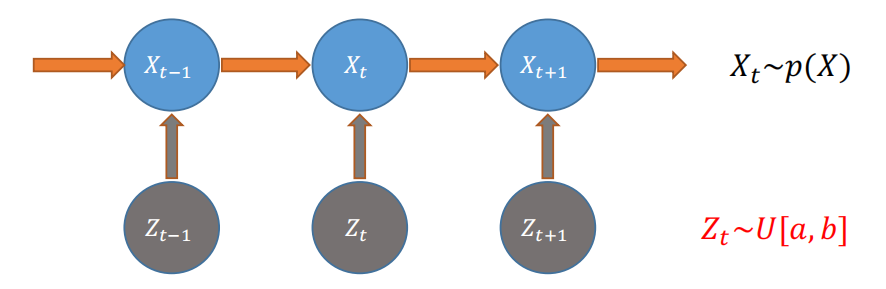
经典的MCMC采样流程：

初始化：设定马尔可夫链的初始状态$ X_0 = x_0 $；
迭代采样（对每一步$ t $）：
- 基于当前状态$ X_t = x_t $，从建议分布 $ q(x \vert x_t) $ 中采样一个候选状态$ y $；
- 从均匀分布$ U[0,1] $中采样一个随机数$ z $；
- 计算接受概率$ \alpha(x_t, y) = \min\left(1, \frac{p(y)q(x_t\vert y)}{p(x_t)q(y \vert x_t)}\right) $；
- 比较$ z $和$ \alpha $：若$ z < \alpha $，则接受转移（$ X_{t+1} = y $）；否则拒绝转移（$ X_{t+1} = x_t $）。

通过“构造满足细致平稳条件的转移规则（接受/拒绝）”，让马尔可夫链的平稳分布等于目标分布$ p(X) $；当链收敛到平稳后，后续的状态就是$ p(X) $的有效样本。

案例1 : 改进的拒绝/接收采样

下面, 我们 使用MCMC（改进的接受-拒绝采样）从Γ分布中生成样本，使用Metropolis算法

要采样的目标概率密度函数是Γ分布：

\[f(x) = 0.5x^2e^{-x}\]

这个分布无法直接用简单方法采样，因此用MCMC的接受-拒绝逻辑生成样本

N = 40000;                  % 1. 设定采样总次数为40000次
f = inline('0.5*x*x*exp(-x)','x');  % 2. 定义目标分布f(x)
d = zeros(1,N);             % 3. 初始化存储样本的数组d
x = 2;                      % 4. 设定Markov链的初始状态x=2
for i = 1:N                 % 5. 开始迭代采样
    y = x - 1 + 2*rand();   % 6. 从建议分布采样候选状态y：这里用的是“当前x附近的均匀分布”（范围[x-1, x+1]）
    if y < 0                % 7. 保证y非负（因为Γ分布的x≥0）
        y = x;              % 若y<0，拒绝这个候选，保持y=x
    end
    h = min(1, f(y) / f(x));% 8. 计算接受概率h：取“f(y)/f(x)”和1的较小值（避免概率大于1）
    U = rand;               % 9. 从均匀分布U[0,1]采样随机数U
    if (U < h)              % 10. 比较U和h：若U<h，接受候选状态y
        x = y;
    end
    d(i) = x;               % 11. 记录当前状态x（无论是否转移，都存入样本数组）
end
a = 0:0.08:20;              % 12. 设定直方图的区间
hist(d(floor(N / 2):end), a);  % 13. 绘制后20000个样本的直方图（前半部分是“燃烧期”，丢弃以保证样本是平稳分布）

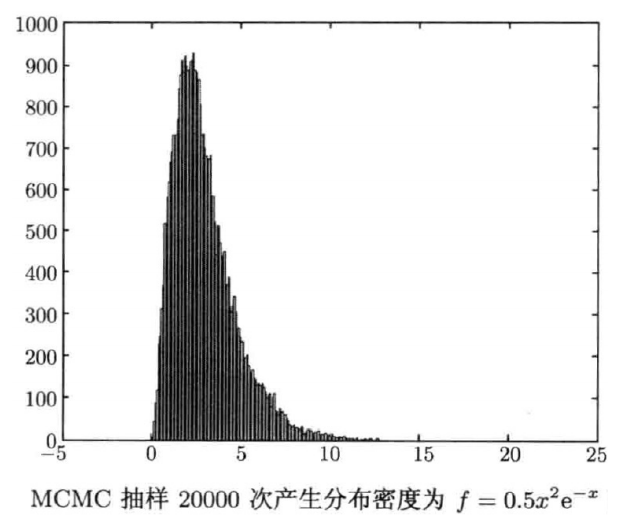
直方图是采样20000次（取后20000个样本）的结果，形状与目标Γ分布$ 0.5x^2e^{-x} $一致，说明MCMC采样成功生成了该分布的样本。

问题1 为什么这样做是对的？

那么为啥这样就一定能产生我们想要的分布嘞。

我们知道马尔科夫链收敛的充分条件是细致平衡条件。即如果一个分布 $\pi(x)$ 和马尔可夫链的转移概率 $P(y	x)$，满足：
$$ \pi(x) P(y	x) = \pi(y) P(x	y) $$
则称 $\pi(x)$ 和 $P(y	x)$ 满足细致平衡。满足细致平衡则一定满足平稳分布，只要能构造出满足上式的转移概率$P(y	x)$，那么$\pi(x)$必然是这条链的平稳分布；在代码里，最终存储的数组`d`，就是收敛后的链状态。

此外，MCMC的核心任务是人为设计转移概率 $P(y

x)$，让它和我们的目标分布 $f(x)$ 满足细致平衡条件。代码里的建议分布+接受概率，本质就是在设计这个满足细致平衡的转移概率 $P(y

x)$。也就是说，我们的目标就是让构造的马尔可夫链的平稳分布 = Γ分布 $f(x)=0.5x^2e^{-x}$。

问题2 为什么选均匀分布作为建议分布？

补充说明一下，在上面的代码中，建议分布可以换，比如正态分布 $y \sim N(x, \sigma^2)$（x为均值，固定方差），也是对称的，效果更好，比如把代码行6改成 y = x + randn()。

在现在的代码中，y = x -1 + 2*rand() → 等价于 $y \sim Uniform(x-1, x+1)$，这个分布在MCMC里叫 建议分布(Proposal Distribution)，记为 $Q(y x)$：表示「在当前状态x时，生成候选状态y的概率」。

Metropolis对建议分布的唯一要求是「对称」即 $$ Q(y

x) = Q(x

y) $$ ，从x到y的建议概率 = 从y到x的建议概率。而均匀分布满足这个条件，如果y在 $[x-1,x+1]$ 里，那么x一定在 $[y-1,y+1]$ 里，二者的建议概率完全相等。

问题3 为什么接受概率是 $h=min(1, \frac{f(y)}{f(x)})$ ？（代码行8）【核心核心】

这是Metropolis算法最精髓的一步，也是「为什么最终能得到正确分布」的关键！这一行代码，直接决定了我们构造的马尔可夫链，能满足「细致平衡条件」。

分两种情况讨论（无数学门槛，很好理解）：

情况1：$f(y) \ge f(x)$ → $\frac{f(y)}{f(x)} \ge 1$ → $h=1$ 此时接受概率为1，意味着必然接受候选y。对应的，从y到x的接受概率 $h(x|y)=min(1, f(x)/f(y)) = f(x)/f(y)$。代入细致平衡公式： $f(x) \cdot Q(y|x) \cdot 1 = f(y) \cdot Q(x|y) \cdot \frac{f(x)}{f(y)}$ 因为$Q(y|x)=Q(x|y)$，两边化简后完全相等 ✔️。
情况2：$f(y) < f(x)$ → $\frac{f(y)}{f(x)} < 1$ → $h=f(y)/f(x)$ 此时接受概率是比值本身，意味着以概率h接受候选y。对应的，从y到x的接受概率 $h(x|y)=min(1, f(x)/f(y)) = 1$。代入细致平衡公式： $f(x) \cdot Q(y|x) \cdot \frac{f(y)}{f(x)} = f(y) \cdot Q(x|y) \cdot 1$ 同样因为$Q(y|x)=Q(x|y)$，两边化简后完全相等 ✔️。

因此，只要用这个接受概率，就一定能让目标分布$f(x)$成为马尔可夫链的平稳分布！这就是你代码里这一步的数学正确性根源，没有这个接受概率，一切都是空谈。

问题4 为什么要采样U~U[0,1]，并比较U<h？（代码行9-10）

原因非常简单：

若要让一个事件以概率$h$发生，只需从[0,1]的均匀分布中采样一个随机数U，如果U<h，则事件发生；否则不发生。

问题5 为什么无论是否接受，都要把x存入样本数组？（代码行11）

马尔可夫链的「每一个状态」都是链的一部分，拒绝候选y → 链的状态没有发生转移，当前状态还是x，这个x本身就是链的一个有效状态；接受候选y → 链的状态转移到y，这个y是链的下一个有效状态。

样本数组d存储的，是马尔可夫链的每一个状态值，而不是「只存储被接受的候选值」。如果只存被接受的，样本序列就断了，也不再是马尔可夫链的状态序列，自然无法收敛到平稳分布。

问题6 为什么要「丢弃前半部分样本（燃烧期）」？（代码行13）

这是MCMC采样的必做步骤，也是你理解「收敛」的关键，回答你：为什么不是所有样本都能用？

燃烧期(Burn-in)的定义：马尔可夫链从「初始值x=2」出发，前若干次迭代的状态，还没有收敛到平稳分布，这些状态值服从的是「初始值附近的分布」，而不是目标分布$f(x)$，这段迭代期就是燃烧期；
核心原因：马尔可夫链的收敛是「渐进的」，不是一蹴而就的。初始值x=2只是一个起点，前几千/几万次迭代，链的状态还在「探索」目标分布的形状，样本的分布和Γ分布差异很大；
你的代码逻辑：总采样40000次，丢弃前20000次，只用后20000次。这是经验最优值，保证后一半样本已经完全收敛，服从目标分布。

补充：如果初始值选得离目标分布的峰值很近，燃烧期可以更短；如果选得很远，需要更长的燃烧期。但无论如何，丢弃前半部分是最稳妥的做法。

问题7 为什么这个案例是Γ分布？

Γ分布的标准形式是：$f(x) = \frac{1}{\Gamma(\alpha)\beta^\alpha}x^{\alpha-1}e^{-x/\beta}, x\ge0$ 你的目标分布：$f(x)=0.5x^2e^{-x}$ → 对应 $\alpha=3, \beta=1$，因为 $\Gamma(3)=2! = 2$，所以 $\frac{1}{\Gamma(3)1^3} = 0.5$，完全匹配。 → 你采样的是Γ(3,1) 分布，这也是为什么样本的取值集中在2~6之间，符合Γ分布的形状。

模拟 “掷双骰子点数和” 的分布

这个例子是用MCMC的“极小邻域法”模拟“掷双骰子点数和”的分布（目标分布是双骰子点数和的概率分布），具体逻辑和步骤如下：

掷两个骰子，点数和$ x $的可能取值是2~12，其未归一的概率密度$ f(x) $（对应出现的次数）为：

$ x $	2	3	4	5	6	7	8	9	10	11	12
$ f(x) $	1	2	3	4	5	6	5	4	3	2	1

我们先用MCMC的极小邻域法生成这个分布的样本。

极小邻域法的核心是为每个状态$ x $定义“只在相邻状态转移”的建议分布$ g(y|x) $：

对当前状态$ x $，候选状态$ y $只能是“$ x-1 $”或“$ x+1 $”（边界状态做限制：$ x=2 $时只能转移到3，$ x=12 $时只能转移到11）；
转移到相邻状态的概率各为$ 1/2 $，即：

\[g(y\vert x) = \begin{cases} 1/2, & y = \max\{x-1, 2\} \quad (\text{左邻域}) \\ 1/2, & y = \min\{x+1, 12\} \quad (\text{右邻域}) \\ 0, & \text{其他} \end{cases}\]

对应的建议分布矩阵$ G $（行是当前状态，列是候选状态）中，只有“当前状态±1”的位置为$ 1/2 $，其余为0（比如状态2的建议分布是“2→2（实际是$ \max(2-1,2)=2 $）和2→3，各1/2”）。

代码通过MCMC的“建议-接受”逻辑生成样本，步骤如下：

f = [1,2,3,4,5,6,5,4,3,2,1];  % 1. 目标分布的未归一密度（对应x=2~12）
d = zeros(1,50000);            % 2. 存储50000个样本的数组
x = 5;                         % 3. 初始化Markov链的初始状态（比如x=5）
for i = 1:50000                % 4. 迭代采样
    U = rand();                % 5. 采样均匀分布随机数，决定转移方向
    if (U < 0.5)
        y = max(x - 1, 2);     % 左邻域：x-1，最小不小于2
    else
        y = min(x + 1, 12);    % 右邻域：x+1，最大不大于12
    end
    % 6. 计算接受概率：f(y)/f(x)与1的较小值（f是未归一密度，不影响比例）
    h = min(1, f(y - 1) / f(x - 1));  % 注：f的索引是y-2+1=y-1（因为x从2开始）
    U = rand();                % 7. 再采样一个均匀分布随机数
    if (U < h)                 % 8. 若U<h，接受转移；否则保持当前状态
        x = y;
    end
    d(i) = x;                  % 9. 记录当前状态为样本
end
% 10. 绘制后20000个样本的直方图（丢弃前30000个“燃烧期”样本）
histogram(d(30000:end), 2:12);

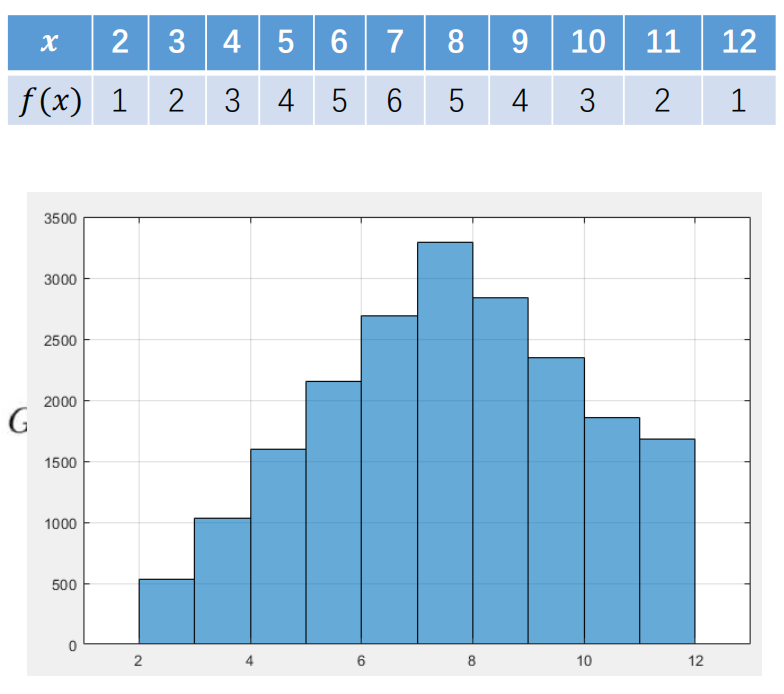
直方图的形状与双骰子点数和的目标分布（中间7最高，向两边递减）一致，说明极小邻域法成功生成了目标分布的样本。

我们再使用极大邻域法解决这个问题.

极大邻域法的建议分布是从当前状态可以等概率转移到所有可能状态：双骰子点数和的状态是2~12（共11个状态），因此建议分布矩阵$ G $的每个元素都是$ \frac{1}{11} $，即： $G = \begin{pmatrix} \frac{1}{11} & \frac{1}{11} & \dots & \frac{1}{11} \\ \frac{1}{11} & \frac{1}{11} & \dots & \frac{1}{11} \\ \vdots & \vdots & & \vdots \\ \frac{1}{11} & \frac{1}{11} & \dots & \frac{1}{11} \end{pmatrix}$ 含义：从任意当前状态$ x $，候选状态$ y $可以是2~12中的任意一个状态，且每个状态的转移概率都是$ \frac{1}{11} $。

代码通过“全状态随机建议+接受-拒绝”生成样本，步骤如下：

f = [1,2,3,4,5,6,5,4,3,2,1];  % 1. 目标分布的未归一密度（对应x=2~12）
d = zeros(1,40000);            % 2. 存储40000个样本的数组
x = 5;                         % 3. 初始化Markov链的初始状态（比如x=5）
for i = 1:40000                % 4. 迭代采样
    % 5. 从所有状态（2~12）中等概率采样候选状态y：randi(11,1)生成1~11，+1后得到2~12
    y = randi(11, 1) + 1;      
    % 6. 计算接受概率：f(y)/f(x)与1的较小值（f是未归一密度，比例不变）
    h = min(1, f(y - 1) / f(x - 1));  % 注：f的索引是y-2+1=y-1（x从2开始）
    U = rand();                % 7. 采样均匀分布随机数U~U[0,1]
    if (U < h)                 % 8. 若U<h，接受转移；否则保持当前状态
        x = y;
    end
    d(i) = x;                  % 9. 记录当前状态为样本
end
% 10. 绘制后10000个样本的直方图（丢弃前30000个“燃烧期”样本）
hist(d(30000:end), 1:11);

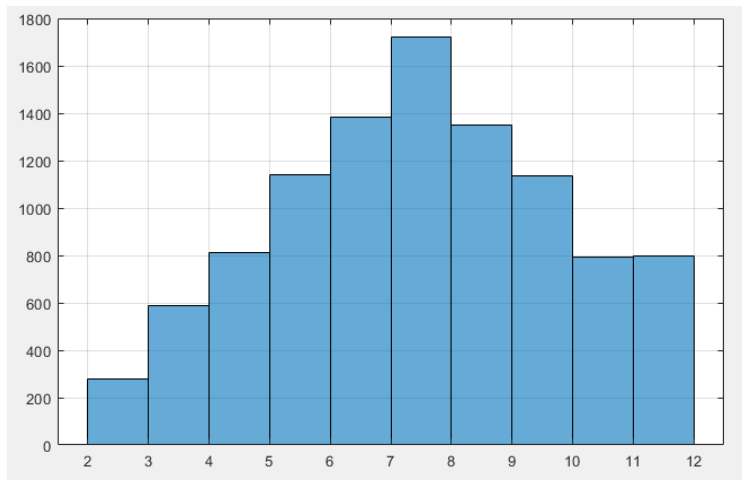
直方图的形状与双骰子点数和的目标分布（中间7最高，向两边递减）一致，说明极大邻域法也成功生成了目标分布的样本。

极小邻域法 仅在相邻状态间转移（建议分布是局部的）；极大邻域法 在所有状态间等概率转移（建议分布是全局的）；两者都通过“接受概率”保证链的平稳分布匹配目标分布，只是建议分布的范围不同。

8.3.1 Metropolis–Hastings 采样

Metropolis–Hastings（简称M-H）采样是最经典的MCMC方法之一，用于从复杂概率分布中生成样本.

M-H采样的核心是构造“接受概率”，保证马尔可夫链的平稳分布等于目标分布$ f(x) $（或$ p(x) $）。接受概率的公式为： $h(x, y) = \min\left\{1,\ \frac{f(y) \cdot g(x \vert y)}{f(x) \cdot g(y \vert x)}\right\}$ 其中$ x $是当前状态，$ y $是从建议分布$ g(y \vert x) $中采样的候选状态；$ g(x \vert y) $是从候选状态$ y $转移回$ x $的建议分布概率。

具体算法如下

初始化：设定马尔可夫链的初始状态$ X_0 = x_0 $；
迭代采样（对每一步$ t $）：
- 基于当前状态 $ X_t = x_t $，从建议分布 $ g(y \vert x_t) $中采样候选状态$ y $；
- 从均匀分布 $ U[0,1] $ 中采样随机数 $ u $；
- 计算接受概率 $ h(x_t, y) = \min\left{1,\ \frac{f(y)g(x_t \vert y)}{f(x_t)g(y x_t)}\right} $；
- 若 $ u < h(x_t, y) $，接受转移（令$ X_{t+1} = y $）；否则拒绝转移（令$ X_{t+1} = x_t $）。

M-H是Metropolis算法的推广, Metropolis算法 是M-H的特殊情况，要求建议分布是对称的（即$ g(y \vert x) = g(x

y) $），此时接受概率简化为：

\[h(x, y) = \min\left\{1,\ \frac{f(y)}{f(x)}\right\}\]

M-H算法 将建议分布推广到非对称情形（只需满足“可逆性”：$ g(y \vert x) > 0 \iff g(x

y) > 0 $），适用范围更广。

来自课本的伪代码

证明Metropolis算法有效

只需验证Markov链的细致平衡条件成立。即需验证 $f(x)h(x,y) = f(y)h(y,x).$

证明(来自课本6.4 P122):

我们可以把概率密度分布想象为有数目很大的一群行人分处在各个状态位置上形成的人数分布，在每一时间步，每个行走者都在空间 $\Omega$ 中从不同的目前状态位置相互独立地行走。我们记 $m_t(x)$ 为：经过 $t$ 步行走之后处在 $x$ 状态位置的行走者的数目。那么第 $t+1$ 步，从 $x$ 状态到 $y$ 状态的行走者的数目与反方向的行走者的数目之差为 $\begin{aligned} \delta_{xy} &= m_t(x)P(x \to y) - m_t(y)P(y \to x) \\ &= m_t(y)P(x \to y)\left( \frac{m_t(x)}{m_t(y)} - \frac{P(y \to x)}{P(x \to y)} \right), \end{aligned}$ 其中 $P(x \to y)$ 是在 $x$ 状态处的行走者行走到 $y$ 状态的概率，$P(y \to x)$ 是在 $y$ 状态处的行走者行走到 $x$ 状态的概率。

如果足够大的迭代次数 $t$ 能够使得 Metropolis 算法生成的马尔可夫链达到稳定分布，则行走者处在各状态的数目分布 $m_t(x)$ 应满足动态平衡性：$\delta_{xy}=0$。记达到平衡时在 $x$ 状态处的行走者的数目为 $m_e(x)$，于是有 $\frac{m_e(x)}{m_e(y)} = \frac{m_t(x)}{m_t(y)} = \frac{P(y \to x)}{P(x \to y)} \tag{6.11}$

接下来我们证明：$m_e(x) \propto f(x)$。在 Metropolis 算法中，由 $x$ 到 $y$ 的转移概率为 $P(x \to y) = g(y|x)h(x,y)$

这个式子是因为, 由建议分布$ g(y x) $生成一个候选状态$ y $，$ g(y x) $表示“从当前状态$ x $出发，生成候选状态$ y $的概率”。用接受概率$ h(x,y) $判断是否接受这个候选状态$ y $，$ h(x,y) = \min\left{1, \frac{f(y)}{f(x)}\right} $（Metropolis准则），表示“接受候选状态$ y $的概率”。

根据算法的对称性条件，有 $g(y|x) = g(x|y)$，那么 $\frac{m_e(x)}{m_e(y)} = \frac{P(y \to x)}{P(x \to y)} = \frac{h(y,x)}{h(x,y)}$

由 Metropolis 算法的判别准则： (1) 如果 $f(x) > f(y)$，则 $h(y,x)=1$，这时由 $x$ 转移到 $y$ 且被接受的概率为 $\frac{m_e(x)}{m_e(y)} = \frac{1}{h(x,y)} = \frac{f(x)}{f(y)}$

(2) 如果 $f(y) \geq f(x)$，则 $h(x,y)=1$，这时由 $x$ 转移到 $y$ 且被接受的概率为 $\frac{m_e(x)}{m_e(y)} = \frac{h(y,x)}{1} = \frac{f(x)}{f(y)}$

因此，这就证明了：$m_e(x) \propto f(x)$。

上面的动态平衡式 (6.11) 可以将 $m_e$ 换成 $f$，则该式就是所谓的细致平衡关系： $f(x)P(x \to y) = f(y)P(y \to x) \tag{6.12}$

我们可以直接验证上面设计的对称 Metropolis 算法，使得这个细致平衡关系成立。因为对称性，这只需要验证： $f(x)h(x,y) = f(y)h(y,x) \tag{6.13}$ 显然，重复上面证明过程中的步骤 (1) 和 (2)，即得所证。

最后，我们需要证明该 Metropolis 算法产生的马尔可夫链能够达到稳定分布，从而随着迭代次数的增加，它们渐近趋向于目标概率密度函数 $f$。这只要说明，该算法所隐含的转移是不可约的和非周期性的即可。显然，由建议概率密度函数 $g$ 的构造可知转移是遍历的，故是不可约的。因为 $f$ 存在至少一个最大点 $y^$，使得对所有的 $x$ 有 $f(y^) \geq f(x)$，则在迭代过程中至少会有一个状态转移到 $y^*$ 处并有可能留在那里，所以这样的链不能成为周期性的。到此，我们完成了 Metropolis 算法的证明。

8.3.2 MCMC的其他性质

MCMC遍历性定理

MCMC的遍历性定理是保证MCMC能用于计算目标分布期望的核心理论，它明确了“马尔可夫链的样本均值可以收敛到目标分布期望”的条件和结论，具体解释如下：

要应用遍历性定理，马尔可夫链需要满足： 1. 不可约：任意两个状态之间可以通过有限步转移到达（状态连通）； 2. 非周期：状态的周期为1（不会陷入固定间隔的循环）； 3. 平稳分布为 $\pi$：马尔可夫链收敛到目标分布$\pi$。

若马尔可夫链满足上述条件，且$\xi: \Omega \to \mathbb{R}$是任意一个关于状态的函数（比如状态的某个统计量），则当样本数$N$趋于无穷大时， 样本均值会收敛到目标分布$\pi$下的期望 ：

\[\lim_{N \to \infty} \frac{1}{N} \sum_{i=1}^N \xi(x_i) = E_{\pi}(\xi)\]

其中：

$x_1, x_2, \dots, x_N$是马尔可夫链达到平稳后生成的样本；
$E_{\pi}(\xi)$是函数$\xi$在目标分布$\pi$下的期望。

遍历性定理解决了MCMC的“实用价值”问题, 仅让马尔可夫链收敛到平稳分布还不够，遍历性保证了用平稳后的样本计算的均值，能逼近目标分布的期望.

MCMC收敛性与稳定性

传统独立采样的收敛性. 对于独立同分布（i.i.d.）的样本（比如从分布中直接抽取的$ X_1,X_2,\dots,X_n $）：用样本均值估计分布的未知期望$ \mu = E(X) $：

\[\bar{X}(n) = \frac{1}{n} \sum_{j=1}^n X_j\]

样本均值的方差随样本量增大而减小：

\[Var(\bar{X}(n)) = \frac{\sigma^2}{n} \quad (\sigma^2是分布的方差)\]

由中心极限定理，样本均值的标准化形式会渐进服从正态分布：

\[Z_n = \frac{\sqrt{n}}{\sigma} (\bar{X}(n) - \mu) \xrightarrow{n\to\infty} \mathcal{N}(0,1)\]

即当样本量足够大时，样本均值与真实期望的偏差会近似服从标准正态分布。

MCMC采样的样本是马尔可夫链的状态（不是独立同分布的），但遍历性定理保证了：

当马尔可夫链满足“不可约、非周期、收敛到平稳分布”时，平稳后的样本均值也会收敛到目标分布的期望（类似传统采样的样本均值收敛）；
同时，MCMC样本的“渐进正态性”也成立（只是方差需要考虑马尔可夫链的相关性，会引入额外的“自相关系数”修正，但核心收敛逻辑与传统采样一致）。

MCMC的“收敛性”指样本均值收敛到目标分布的期望，“稳定性”指样本均值的波动随样本量增大而减小，且渐进服从正态分布——这与传统独立采样的收敛逻辑一致，只是MCMC是通过马尔可夫链的平稳性实现的。

MCMC误差估计

MCMC的误差估计是基于中心极限定理，量化“样本均值估计目标分布期望”的随机误差，核心逻辑是用“置信区间”来描述估计的不确定性.

MCMC的误差是随机性误差（和普通数值方法的确定性误差不同），因为MCMC样本是马尔可夫链生成的随机样本，估计结果会随样本不同而波动。

利用勒维-林德伯格中心极限定理，当MCMC样本量$ n \to \infty $时，样本均值$ \bar{X}(n) $与目标期望$ \mu $的偏差满足：

\[\lim_{n \to \infty} \text{Pr}\left( (\bar{X}(n) - \mu) \leq X_{\alpha} \frac{\sigma}{\sqrt{n}} \right) = \frac{1}{\sqrt{2\pi}} \int_{-X_{\alpha}}^{X_{\alpha}} \exp\left(-\frac{t^2}{2}\right) dt = 1 - \alpha\]

其中：

$ \sigma^2 $是目标分布的方差；
$ X_{\alpha} $是正态差（对应标准正态分布的分位数，比如$ \alpha=0.05 $时，$ X_{\alpha}\approx1.96 $）；
$ \alpha $是置信概率（显著水平），$ 1-\alpha $是置信水平（比如$ 1-\alpha=0.95 $表示“有95%的概率，偏差不超过$ X_{\alpha}\frac{\sigma}{\sqrt{n}} $”）。

MCMC估计的绝对误差（样本均值与真实期望的偏差上限）为：

\[\varepsilon_{\alpha} = \left| \frac{1}{n}\sum_{i=1}^n X_i - \mu \right| = X_{\alpha} \frac{\sigma}{\sqrt{n}}\]

即在置信水平$ 1-\alpha $下，样本均值与真实期望的偏差不会超过$ X_{\alpha}\frac{\sigma}{\sqrt{n}} $。

简言之，MCMC的误差估计是通过中心极限定理，用“正态分布的分位数+分布方差+样本量”来量化估计的随机误差，最终得到一个有概率保证的误差上限。

9 模拟退火 – 统计物理

9.1 模拟退火的基本思想

模拟退火的基本思想是模拟金属退火的物理过程：高温时金属原子活跃（可随机移动），低温时逐渐稳定（原子排列趋于有序）；对应到优化问题中，通过“虚拟温度”控制搜索的随机性，在高温时接受较差解以跳出局部最优，低温时逐步收敛到全局最优。

物理类比与能量函数 把优化问题的目标函数 $ f(x) $ 看作“能量”，系统状态（解）的概率服从玻尔兹曼分布： $\frac{1}{Z} e^{-\frac{f(x)}{k_B T}}$ （$ Z $ 是归一化因子，$ T $ 是虚拟温度）。温度越高，“能量高的状态（差解）”被接受的概率越大。
状态转移的拒绝-接受准则 从当前解 $ x $ 随机生成新解 $ y $ 后，按以下规则决定是否接受：
- 若 $ f(y) \leq f(x) $（新解更优）：直接接受 $ y $；
- 若 $ f(y) > f(x) $（新解更差）：以概率 $ e^{-\frac{f(y)-f(x)}{k_B T}} $ 接受 $ y $（温度越高，接受差解的概率越大）。

也就是从当前$x$到新状态$y$的接受概率 $h(x,y) = \min \left\{1, e^{-\frac{f(y)-f(x)}{k_B T}} \right\}$

算法流程
1. 随机选初始解 $ s $，初始化温度 $ T $；
2. 循环（直到停止条件）：
  - 在当前温度下，多次随机生成邻域解 $ s’ $，按“拒绝-接受准则”更新解，直到系统达到“热平衡”；
  - 降低温度 $ T $；
3. 返回找到的最优解。
关键性质（保证全局最优）
- 不可约性：任意两个解之间，有限步内总能互相到达（避免搜索陷入局部区域）；
- 对称性：状态转移概率满足 $ g(x y)=g(y x) $（保证搜索的无偏性）。

模拟退火是通过“温度调控随机性”的随机搜索算法：高温“探索”（接受差解），低温“利用”（收敛到优解），最终逼近全局最优。

9.2 超参数T的选择建议

开始温度$T_0$要足够大，通常可以取100至2000
衰减的速率要小 (a) 典型冷却衰减方式：$T_{k+1} = \alpha T_k, k = 0,1,2,…,$ 其中，常数$0 < \alpha < 1$; $\alpha$控制降温的速率，$\alpha \in (0.5, 0.99)$取值越大速率越小。 (b) 逆对数的冷却方式：$T = \frac{c}{a+\ln t}$，其中$a$和$c$是常数且$c$通常取很大的正数。
合适的链长 & 停止温度$T_f$应设为足够小(经验值 0.01~5)

9.3 旅行商问题

结合旅行商问题（TSP）的场景，模拟退火的Metropolis抽样算法（以“部分路径逆转”为邻域操作）可以整理为以下步骤

9.3.1 算法输入

城市集合：$ C_1,C_2,…,C_n $（含坐标，用于计算距离 $ d(C_i,C_j) $）
温度参数：初始温度 $ T_0 $、终止温度 $ T_f $、温度衰减规则 $ T(t) $（如 $ T(t+1) = \alpha \cdot T(t),\ 0<\alpha<1 $）

9.3.2 算法步骤

初始化
- 生成初始路径：随机生成 $ {2,3,…,n} $ 的一个置换 $ x $（对应线路 $ C_1 \rightarrow C_{i_1} \rightarrow C_{i_2} \rightarrow … \rightarrow C_{i_{n-1}} \rightarrow C_1 $）。
- 计算初始路径长度（能量）：$ E(x) = \sum_{k=1}^{n-1} d(C_{i_{k-1}},C_{i_k}) + d(C_{i_{n-1}},C_1) $（其中 $ i_0=1 $）。
- 初始化变量：当前温度 $ T = T_0 $，最优路径长度 $ B = E(x) $，迭代计数 $ t=0 $。
主循环（直到 $ T = T_f $）
- 生成邻域解（Metropolis抽样）：随机选择当前路径 $ x $ 中的两个城市 $ i_{k_1},i_{k_2} $，逆转这两个城市之间的路径段，得到新路径 $ y $（例如：$ 3→5→2→8→4→6→7 $ 逆转“2-6”后得到 $ 3→5→6→4→8→2→7 $）。
- 计算能量差：计算新路径长度 $ E(y) $，得到 $ \Delta E = E(y) - E(x) $。
- 拒绝-接受准则：计算接受概率 $ h = \min\left{1, e^{-\frac{\Delta E}{T}}\right} $；生成均匀随机数 $ r \sim U(0,1) $，若 $ r < h $，则接受新路径：$ x = y $，$ E(x) = E(y) $。
- 更新最优解：$ B = \min{B, E(x)} $。
- 降温与迭代：$ t = t+1 $，按规则更新温度 $ T = T(t) $。
输出循环结束后，输出最优路径长度 $ B $ 及对应的路径。

9.4 背包问题

9.5 顶点染色问题

10 仿真优化算法 – 非线性优化

10.1 遗传算法

一种模拟生物在自然环境中的遗传和进化的过程而形成的自适应全局优化概率搜索算法

五个核心要素：参数编码、种群初始化、遗传算子设计、适应度函数设计、控制参数

求shekel函数最小值

Shekel函数在这里是一个单变量测试函数，常用于优化算法（比如遗传算法）的性能测试，它的用法可以从这几个方面理解：

先把shekel函数保存为.m文件（比如shekel.m），代码功能是计算输入x对应的函数值：

function y = shekel(x)
    % 输入：x（单个数值或数组）
    % 输出：y（对应x的shekel函数值）
    y = 1./(10.295*(x-7.382).^2 + 0.1613) + ...
        1./(4.722*(x-1.972).^2 + 0.2327) + ...
        1./(10.928*(x-8.111).^2 + 0.2047);
end

这个Shekel函数是求最小值的目标函数（因为优化任务是找它在2≤x≤9的最小值）。

在全局优化中（比如用Matlab的遗传算法ga），它的角色是：

算法会不断尝试不同的x（在2~9区间内），调用shekel(x)计算函数值；
最终找到使shekel(x)最小的x（即“最小点”）和对应的函数值（即“最小值”）。

用Matlab全局优化工具箱的ga（遗传算法）求解时，代码格式是：

[x, v] = ga(@shekel, 1, [], [], [], [], 2, 9);

@shekel：指定目标函数是shekel；
1：变量个数（这里是单变量x）；
中间的[]：遗传算法的约束/参数默认值；
2, 9：变量x的上下界（2≤x≤9）；
输出x：使shekel(x)最小的自变量值；
输出v：对应的最小值（即shekel(x)）。

10.1.1 参数编码

目的: 将优化问题转换为组合问题

常用编码方案: 二进制编码、整数编码、实数编码

1. 二进制编码. 把变量转化为二进制字符串（0和1组成）的形式。

例子：若变量x∈[0,10]，精度到0.1，则需要log2(10/0.1)=7位二进制（比如1010101对应某个x值）。
优势：编码/解码简单、遗传操作（交叉/变异）容易实现、种群多样性好。
劣势：编码长度可能很长（精度越高越长）、不能直接体现变量的实际意义。

2. 整数编码. 把变量直接用整数表示（适用于变量本身是整数的问题）。

例子：求解“安排5个任务的顺序”，变量是任务编号1、2、3、4、5，直接用整数序列[3,1,5,2,4]表示解。
优势：适合整数类优化问题（如调度、排列）、编码简洁。
劣势：只适用于整数变量，不适合连续型变量。

3. 实数编码. 直接用变量的 实际数值(浮点数) 作为编码（适用于连续型变量）。

例子：变量x∈[2,9]，直接用4.86（Shekel函数的最小点）作为编码。
优势：无需编码/解码、能直接反映变量的实际意义、适合连续优化问题。
劣势：遗传操作（如变异）需控制范围（避免偏离解空间）、容易提前收敛（种群多样性不足）。

4. 格雷码

核心特点是“相邻整数对应的编码只有1位不同”，可以优化遗传算法的局部搜索能力。

以“相邻数175和176”为例：

普通二进制编码：0010101111→0010110000（5位不同）；
格雷码编码：0010100100→0010101100（仅1位不同）。

这种特性让遗传算法的局部搜索更平滑：微小的编码变化对应微小的变量变化，避免普通二进制“编码变多位、变量跳变”的问题。

遗传操作（交叉、变异）和普通二进制一样简单；
符合“最小字符集编码”（只用0/1），也适用模式定理分析；
解码时需通过“格雷码→二进制→十进制”的步骤（有固定转换公式）。

10.1.2 初始化种群

初始化种群是遗传算法开始阶段生成初始解集合的步骤，是算法后续进化（交叉、变异等）的基础，核心概念和要点如下：

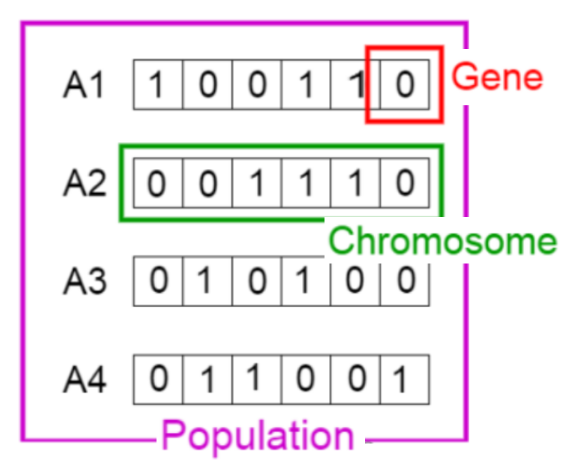
1. 核心概念

遗传算法里用“生物遗传术语”类比优化问题：

基因（Gene）：编码后的最小单元（比如二进制编码里的1位0/1）；
染色体（Chromosome）/个体（Individual）：1个“解”的完整编码（比如A1是一条染色体，由多个基因组成）；
种群（Population）：多个个体（染色体）的集合（比如A1-A4组成一个种群）。

2. 初始化的操作方式

就是生成n个初始个体（染色体），常用2种策略：

策略1（利用先验知识）：如果知道解的大致分布（比如Shekel函数的最小值在4-5附近），就在这个区域内随机生成个体，能加快后续收敛；
策略2（冷启动）：完全随机生成个体（覆盖整个解空间），适合对解分布无了解的情况，之后通过迭代优化。

3. 种群规模的影响

种群里个体的数量（n）要合理设置：

规模过小：种群多样性不足，容易“提前收敛”（没找到全局最优就停了）；
规模过大：计算量会增加，拖慢算法运行速度。

10.1.3 遗传算子

定义三种随机算子, 选择, 重组与变异 .生成状态空间 $ \Omega $ 上的 Markov 链 $X_{t}$ . 可以证明, 通过合适地定义上述三种随机算子，生成的链 {$ X_{t}$} 总是不可约的和非周期的，且收敛于一个稳定分布！

1. 选择(selection)

在遗传算法中，“选择”是从当前种群里挑选优秀个体，让它们进入下一代繁衍的核心操作，目的是保留适应度高（更接近最优解）的个体，推动种群进化。它的核心逻辑是“以适应度为权重，概率性地筛选个体”，常见策略有3种：

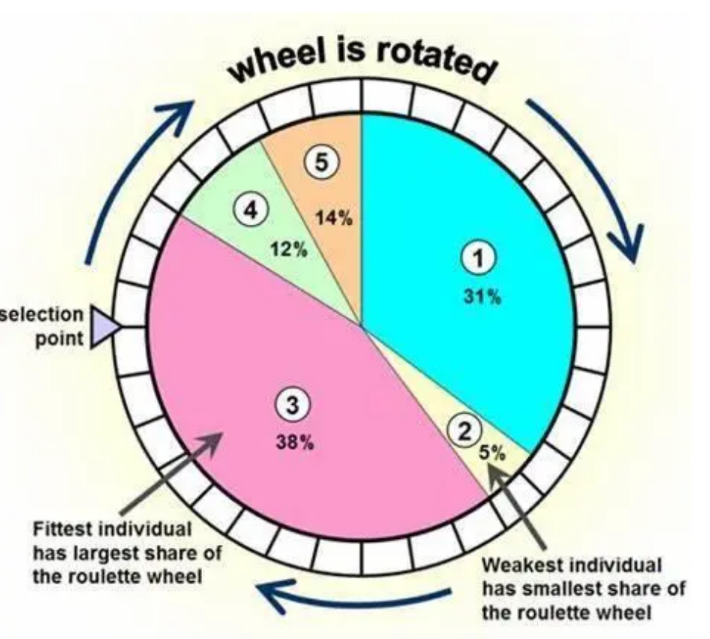
轮盘赌选择策略. 把种群的“适应度总和”比作一个“轮盘”，每个个体的适应度占轮盘的“扇形面积比例”，就是它被选中的概率。例如, 适应度高的个体（如图中“3”）占比38%，被选中的概率远高于适应度低的个体（如“2”仅占5%）。简单直接，但选择误差大, 可能漏掉优秀个体，或选入较差个体。

随机竞争选择. 先按轮盘赌选2个个体，再让这两个个体“竞争”——适应度高的那个被选中，重复这个过程直到选满种群规模。类似“淘汰赛”，能减少轮盘赌的随机误差，更倾向选优秀个体。

最佳保留选择. 分两步： ① 先按轮盘赌选大部分个体； ② 把当前种群中适应度最高的个体直接复制到下一代（避免优秀个体被随机操作淘汰）。

特点：既能保留优秀个体，又兼顾种群多样性，是常用的“保优”策略。

2. 交叉(crossover)

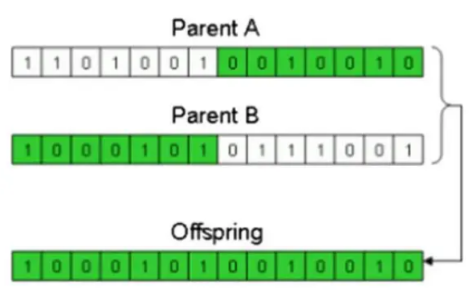
二进制编码：通常方式是1步交叉，即将父母一方的k位初始序列取代第二个亲本的初始k个位置形成新的数位串，以产生后代，其中位置k被随机选择。

实值编码：先随机选择2个parent，然后选择部分进行交换：比如群体的size是N，先选择最好的M个，就需要在产生N-M个才能维持好种群的大小。假设每个染色体的长度是K，那么先把M个种群中的染色体的第一个基因，按照倍数复制成长度为N-M，接着随机再给这个N-M排序下，组成了N-M个后代的第一个基因，以此类推，就完成了任意2个parent的基因交换和重组。

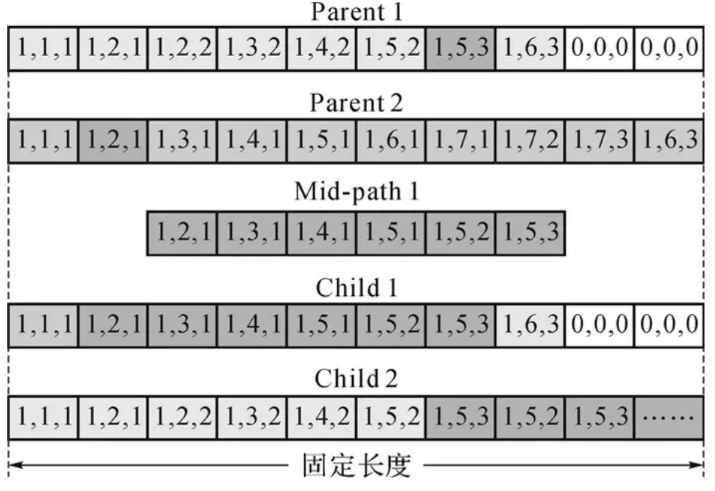
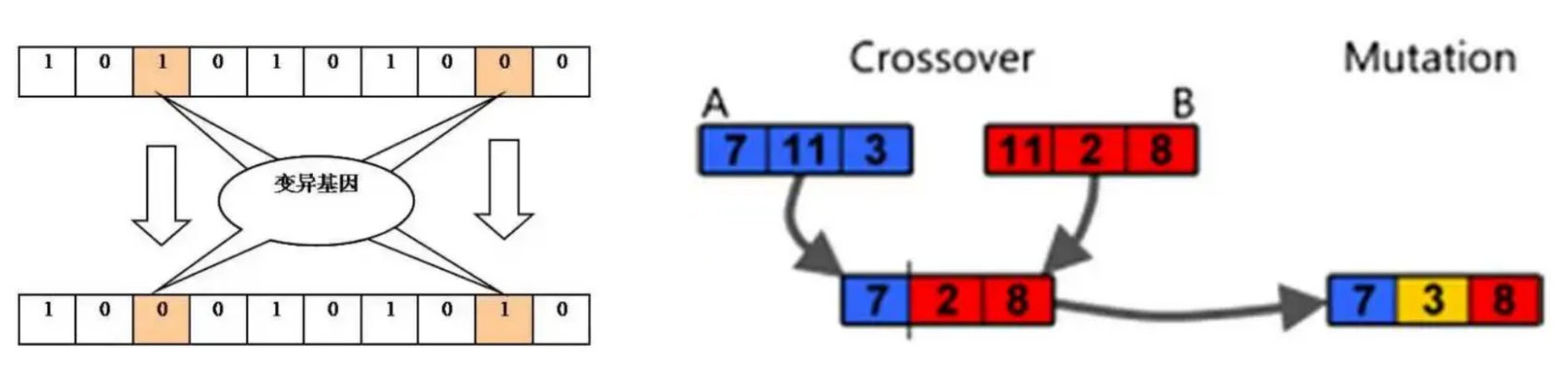
3. 变异(mutation)

二进制编码：随机选择二进制串的一位或多位进行翻转或逆序

实数值编码：遍历N个染色体上的K个基因，然后产生随机数，如果这个随机数小于X，就给这个基因做mutation，如果大于则不更改，具体的实现的时候可以灵活处理。

10.1.4 遗传算法的流程

遗传算法的流程是 生成初始解→迭代优化→输出最优解 的循环过程，核心是通过“选择、交叉、变异”模拟生物进化，逐步找到更优的解。具体步骤（结合图中逻辑）如下：

1. 初始化种群生成一批初始个体（解的编码形式），作为算法的“初始候选解集合”。

2. 计算适应度对种群中每个个体，计算其适应度. 比如求最小值时，函数值越小则适应度越高。遗传算法一般最大化适应度函数.

3. 选择以“适应度为权重”中，从当前种群中筛选出部分个体，作为“繁衍下一代的父/母本”。例如, 依照公式 $ p_i = \frac{f_i}{\sum_{i=1}^n f_i} $ 抽取个体 $x_{i}$ , 其中 $f_i$ 是个体的适应度

4. 遗传（复制、交叉、变异）对选中的个体，按概率执行3种操作（要求 $ p_r + p_c + p_m = 1 $，即三个操作的概率和为1）：

复制（概率 $ p_r $）：直接把优秀个体复制到下一代；
交叉（概率 $ p_c $）：让两个个体交换部分编码（类似“基因重组”），生成新个体；
变异（概率 $ p_m $）：随机改变个体的某一位编码（类似“基因突变”），增加种群多样性。

5. 终止条件判断重复步骤2-4，直到满足终止条件：

达到最大迭代次数/运行时间（比如1万代）；
种群的适应度不再显著变化（说明已接近最优解）。

6. 输出结果终止后，输出种群中适应度最高的个体，作为最终的最优解。

10.1.5 遗传算法的优劣势

优越性：
1. 全局（可能达到）优化
2. 隐含的并行性：编码的不同部分以及不同的操作算子可同时进行
3. 以编码、适应度函数为导向，所需问题背景少、“过程”解释统一
劣势：
1. 过多依赖于适应度函数，但需要使用者自行提供，且无固定标准
2. 群体大小选择不当可能会过早收敛，错过全局最优解
3. 计算参数（群体大小、交换频率、突变频率等）稍有不同可能会得到不同结果
4. 若染色体过长(基因数过多)，群体规模、计算时间急剧增加

10.2 n:m 积和式优化问题

行列式 ($\det(C)$)：我们在计算行列式时，对不同排列的乘积项会根据逆序数的奇偶性加上正号或负号（即公式中的 $\operatorname{sign}(\sigma)$）。 $\det(C) = \sum_{\sigma} \text{sign}(\sigma) \prod_{i=1}^{n} c_{i,\sigma(i)}$

积和式 ($\operatorname{perm}(C)$)：积和式的定义与行列式非常相似，唯一的区别是没有符号项。它将所有排列的乘积直接相加。 $\operatorname{perm}(C) = \sum_{\sigma} \prod_{i=1}^{n} c_{i, \sigma(i)}$ 简单来说，就是从矩阵的每一行取一个元素，确保这些元素不在同一列，将它们乘起来，然后把所有可能的这种组合加在一起。运算量为 $O(n!)$，这是一个非常巨大的计算量，比行列式的计算难得多。

积和式的性质:

若𝐶中有一个0元素，则积和式中有(n-1)!项为0
若𝐶的某一行或某一列元素为0，则积和式为0
交换矩阵的任意两行（列）不改变积和式的值

$n:m$ 积和式优化问题是一个组合优化问题。

设定：
1. 你有一个 $n$ 阶方阵（$n \times n$ 的格子）。
2. 这是一个 0-1 矩阵（格子里的数字只能是 0 或 1）。
3. 你手里总共有 $m$ 个 “1”（即矩阵中元素为 1 的个数总和是 $m$）。
目标：你需要把这 $m$ 个 “1” 填入 $n \times n$ 的格子中，使得最后计算出来的积和式 ($\operatorname{perm}(C)$) 的值最大。

举个例子, 3:5 积和式问题

下面是一个具体的例子：

$n = 3$：这是一个 3阶矩阵。
$m = 5$：矩阵里总共有 5 个 “1”。
结果：最大积和式是 2。

为什么是 2？让我们看 PPT 中的矩阵例子： $\begin{pmatrix} 1 & 1 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$

如何计算这个矩阵的积和式？ 我们需要找出所有“每行取一个，每列取一个”且元素都为 1 的组合：

取 $c_{11}, c_{22}, c_{33}$ (即 $1 \times 1 \times 1$) = 1
取 $c_{12}, c_{21}, c_{33}$ (即 $1 \times 1 \times 1$) = 1
其他任何组合都会包含至少一个 0（例如 $c_{13}$ 是 0）。

所以，$\operatorname{perm}(C) = 1 + 1 = 2$。

关于矩阵的不唯一性：

\[\text{perm}\begin{pmatrix} 0 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \end{pmatrix} = \text{perm}\begin{pmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{pmatrix} = 2.\]

这里展示了另外两个矩阵，它们的形状不同（行或列交换了），但积和式的结果也是 2。这对应了左下角框中的性质 3：“交换矩阵的任意两行（列）不改变积和式的值”。这意味着在优化问题中，我们关心的是 1 的相对结构（比如是否形成了紧密的块状），而不是它们的绝对位置。

$n:m$ 积和式优化问题就是在问：给定 $n \times n$ 的空间和 $m$ 个资源（1），如何布局这些资源，才能让“全排列匹配”的路径数量最多？

如果 $m < n$，积和式一定是 0（因为无法选出 $n$ 个 1）。
如果 $m = n^2$（全 1 矩阵），积和式是 $n!$。
这个问题的难点在于当 $n < m < n^2$ 时，如何分布这些 1 来最大化结果。

10.2.2 使用遗传算法解积和式优化问题

1. 定义染色体. 用 $m$ 个 1 的 $n$ 阶 0-1 矩阵作为染色体。

回顾编码原则

有意义：应使用能易于与所求问题相关。

最小字符集。

2. 定义适应度函数. 即矩阵的积和式 $\operatorname{perm}()$. 数值越大，说明该个体的“基因”越好，被遗传到下一代的概率就越高。

3. 定义遗传算子（变异和交叉）.

变异：东南西北环绕式的领域交换. 可以看到中心有一个深色格子（代表 1），周围标有 E (East), W (West), N (North), S (South) 的格子。这是一个局部搜索策略。不是在矩阵里随机找个地方把 0 变成 1，而是选中一个现有的 1，将其移动到它相邻（上、下、左、右）的空白位置（0）。这种“微调”可以避免破坏矩阵的整体结构，尝试在局部寻找更优解。

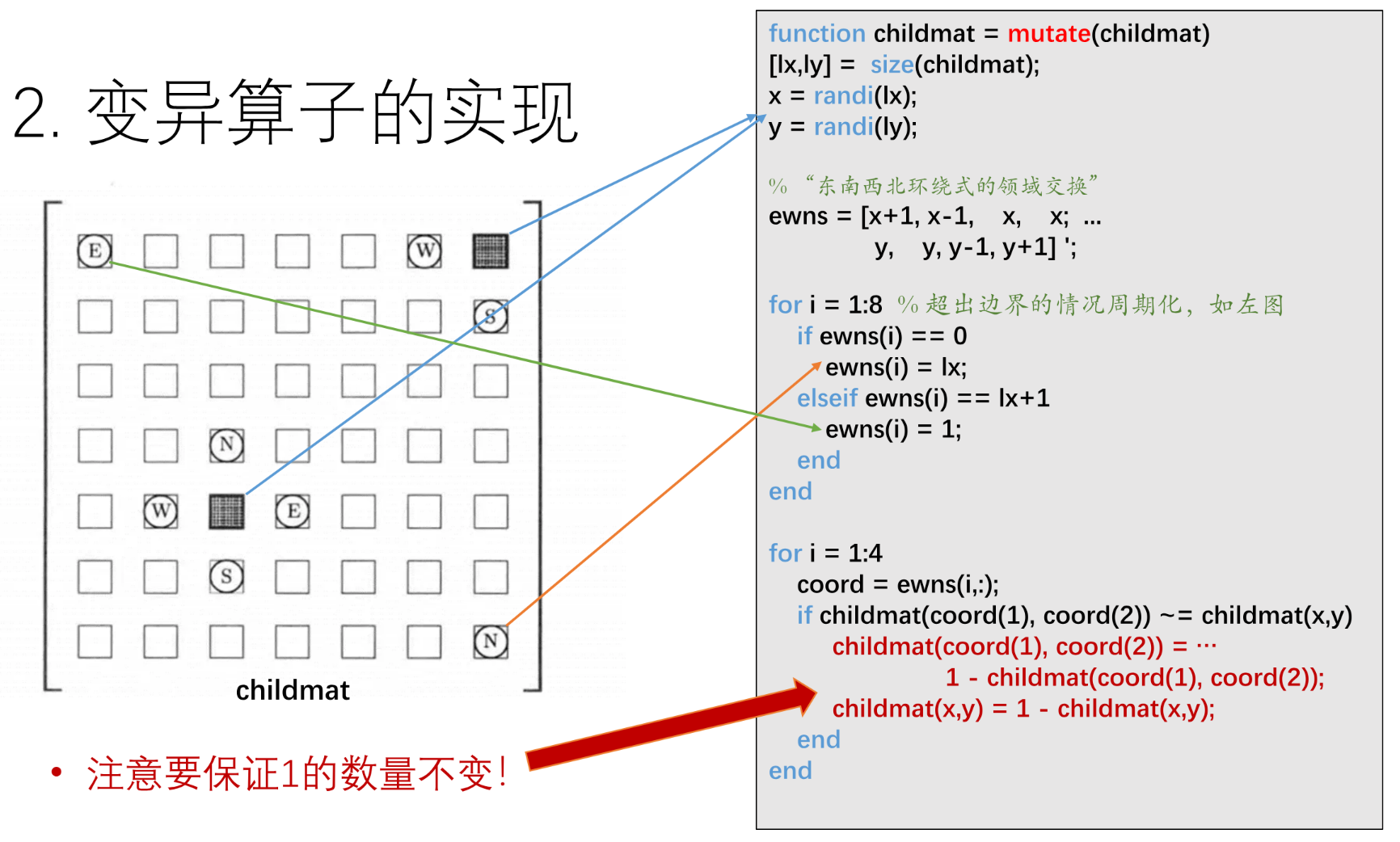
Matlab实现方法

function childmat = mutate(childmat)
[lx,ly] = size(childmat);
x = randi(lx); % 随机生成整数索引。
y = randi(ly);
% “东南西北环绕式的领域交换”
% 构建候选邻居坐标数组
ewns = [x+1, x-1, x, x; y, y, y-1, y+1];  
for i = 1:8 % 超出边界的情况周期化，如左图
    if ewns(i) == 0 % 上面溢出处理, 设为最大值
    ewns(i) = lx;
    elseif ewns(i) == lx+1 % 下面溢出处理, 设为1
    ewns(i) = 1;
    end
end
for i = 1:4 % 交换循环
    coord = ewns(i,:);
    if childmat(coord(1), coord(2)) ~= childmat(x,y)
        childmat(coord(1), coord(2)) = …
        1 - childmat(coord(1), coord(2));childmat(x,y) = 1 - childmat(x,y);
    end
end

Python实现方法, 在python中实现这个可以使用取模运算(%)

def mutation_nsew(matrix):
    """
    基于 PPT 描述的 '东南西北环绕式领域交换' 变异算子。
    """
    rows, cols = matrix.shape
    mutated_matrix = matrix.copy()
    
    # 1. 随机选择一个中心点
    x = np.random.randint(0, rows)
    y = np.random.randint(0, cols)
    
    # 2. 定义东南西北四个方向的偏移量 (dx, dy)
    directions = [
        (-1, 0), # North
        (1, 0),  # South
        (0, -1), # West
        (0, 1)   # East
    ]
    
    # 为了增加随机性，打乱尝试方向的顺序
    np.random.shuffle(directions)
    
    # 3. 遍历邻居并尝试交换
    for dx, dy in directions:
        # 计算邻居坐标，使用取模运算 (%) 实现环绕/穿墙效果
        # 例如：如果 x=-1，python 的 -1 % rows 会自动变成 rows-1 (最后一行)
        nx = (x + dx) % rows
        ny = (y + dy) % cols
        
        # 4. 如果中心点和邻居点的值不同 (即一个是0，一个是1)
        if mutated_matrix[x, y] != mutated_matrix[nx, ny]:
            # 交换两者
            mutated_matrix[x, y], mutated_matrix[nx, ny] = \
                mutated_matrix[nx, ny], mutated_matrix[x, y]
            
            # 变异通常只发生一次即可，交换成功后立即退出
            break
            
    return mutated_matrix

交叉：模板化全局交换. 设矩阵A和B是被选出来进行交换的两个矩阵。首先，将矩阵的元素按行的顺序依次头为相接地排成一维数组，并将数组地头尾连成环绕地形式。然后，随机选出一个共同的起点位置，沿着两个数组的元素向后移动直到第一次出现两个不同的元素，则交换这两个元素，继续沿着数组的元素移动，不断地及进行类似的交换元素，这个过程直至遇到第一次出现不同元素的位置时结束。

Matlab实现方法

function newmat = crossover(mat1, mat2)
[m, n] = size(mat1); % 获取矩阵尺寸
% 一种实现方式，可向量化优化之
for i = 1:m 
    for j = 1:n % 遍历矩阵每一个格子
        if mat1(i, j) ~= mat2(i, j) % 检查两个矩阵在同一位置的值是否不同
            mat1(i, j) = 1 - mat1(i, j);
            mat2(i, j) = 1 - mat2(i, j); % 这是 MATLAB 中常用的位翻转技巧。
            % 如果是 0，1-0=1；如果是 1，1-1=0。这行代码实现了值的交换
        end
    end
end
newmat = mat1;
end

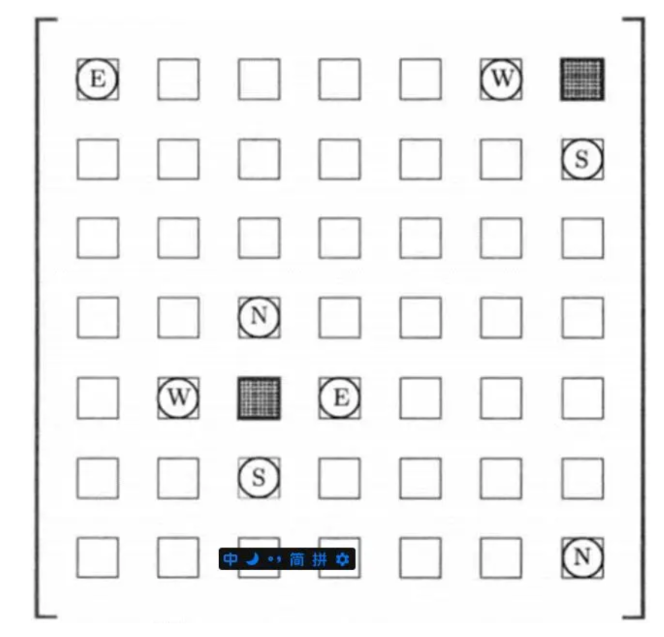
Python实现方法

import numpy as np

def crossover_conserved(parent_a, parent_b):
    """
    基于 PPT 描述的 '模板化全局交换' 交叉算子。
    核心逻辑：在保持 1 的总数不变的前提下交换基因。
    """
    # 复制父代，避免修改原始数据
    child_a = parent_a.copy()
    child_b = parent_b.copy()
    
    rows, cols = parent_a.shape
    # 1. 扁平化：将矩阵展平为一维数组
    flat_a = child_a.flatten()
    flat_b = child_b.flatten()
    total_len = len(flat_a)
    
    # 2. 随机起点
    start_idx = np.random.randint(0, total_len)
    
    # 记录 '1' 的盈亏情况。
    # balance > 0 表示 A 多了 1 (B 少了 1)
    # balance < 0 表示 A 少了 1 (B 多了 1)
    balance = 0 
    
    # 3. 环绕遍历 (最多遍历一圈)
    for k in range(total_len):
        # 环绕索引
        idx = (start_idx + k) % total_len
        
        # 如果两个位置元素不同，尝试交换
        if flat_a[idx] != flat_b[idx]:
            # 执行交换
            flat_a[idx], flat_b[idx] = flat_b[idx], flat_a[idx]
            
            # 更新平衡状态
            # 如果 flat_a 现在变成了 1 (说明原来是 0)，balance + 1
            # 如果 flat_a 现在变成了 0 (说明原来是 1)，balance - 1
            if flat_a[idx] == 1:
                balance += 1
            else:
                balance -= 1
            
            # 4. 终止条件：如果平衡回归为 0，且不仅仅是因为刚开始，说明完成了一次闭环交换
            if balance == 0:
                break
    
    # 将一维数组重新塑形回矩阵
    return flat_a.reshape(rows, cols), flat_b.reshape(rows, cols)

算例主程序

种群参数

popnum = 12; % 种群大小 (Population Size)。每一代有 12 个矩阵个体。
n = 3; % 阶数
m = 5; % 1的个数
maxGen = 1000;
perm_GA(popnum,n,m,maxGen); % 最大迭代次数。繁衍 1000 代后停止。

遗传过程

% 轮盘赌选择(实际上是锦标赛选择, 随机选几个人出来打架，最强的那个胜出)
tournamentSize = 4; %设置大小
for k=1:popnum % 生成新一代 , 我们要生成与上一代数量相同的新个体
    % 选择父代
    tourPopDistances = zeros(tournamentSize, 1); % 建立一个临时名单，用来存参赛选手的成绩。
    % 随机从种群中抽取 4 个幸运观众（randi(popnum) 生成随机索引）
    % 并把他们的适应度（存放在 B 数组中）记录下来
    for i = 1:tournamentSize
        randomRow = randi(popnum);tourPopDistances(i,1) = B(randomRow);
    end 
    % 选择最好的A, 找出这 4 个人里适应度最高的那个数值
    parent1 = max(tourPopDistances);
    % 根据这个最高适应度值，去原始种群矩阵库 mat 中把对应的矩阵实体取出来
    parent1mat = mat(:, :, find(B==parent1, 1)); 
    for i = 1:tournamentSize
        randomRow = randi(popnum);
        tourPopDistances(i,1) = B(randomRow);
    end
    % 选择最好的B
    parent2 = max(tourPopDistances);
    parent2mat = mat(:, :, find(B==parent2, 1)); 
    % 执行交叉
    submat = crossover(parent1mat, parent2mat);
    % 执行变异
    submat = mutate(submat); 
    % 获得新的一代
    offspring(:, :, k) = submat;
end

10.2.3 粘滞现象及修正

粘滞现象 (早熟现象) : 遗传算法在迭代过程中，适应度的改善速度会越来越慢，最终 “陷入” 局部最优解（而不是找到全局最优），这就是粘滞 / 早熟现象。

修正方法: 核心思路是扩大交叉操作的群体范围，打破当前的局部最优束缚; 让当前群体的状态，和整个可选状态空间里的任意 / 随机状态进行交叉，而不是只和当前群体内的个体交叉。引入更多多样性，帮助算法跳出局部最优，向全局最优靠近。

10.2.4 模式定理 (Schema Theorem)

模式定理是遗传算法的核心理论，它解释了 “优秀模式” 在遗传迭代中会指数级增长的规律.

模式（Schema）：是遗传算法中字符串（个体）的 “相似片段”，可以理解为一种具有共性特征的基因片段。
确定位数（阶）：模式中固定字符的数量（越少越好）；
定义长度：模式中第一个和最后一个固定字符的距离（越短越好）；
适应度：模式对应的个体的平均适应度。

在遗传算法的选择、交叉、变异操作作用下, 确定位数少、定义长度短、且平均适应度高于种群平均的模式（即 “优秀模式”），会在子代种群中呈指数级增长。

模式定理的证明:

先明确符号定义

$ m(H,t) $：第$ t $代中，属于模式$ H $的个体数量；
$ p_i = \frac{f_i}{\sum_{i=1}^n f_i} $：个体$ A_i $被选择的概率（适应度越高，概率越大）；
$ \bar{f} = \frac{\sum_{i=1}^n f_i}{n} $：种群的平均适应度；
$ f(H) $：模式$ H $对应的所有个体的平均适应度。

选择操作后模式 $H$ 的数量变化. 当用新种群（非重叠的$ n $个串）代替旧种群时：每个属于模式$ H $的个体，被选中的概率是$ \frac{f(H)}{\sum_{i=1}^n f_i} $（因为模式$ H $的平均适应度是$ f(H) $）。因此，第$ t+1 $代中模式$ H $的数量为：

\[m(H,t+1) = m(H,t) \times n \times \frac{f(H)}{\sum_{i=1}^n f_i}\]

又因为$ \bar{f} = \frac{\sum_{i=1}^n f_i}{n} $，即$ \sum_{i=1}^n f_i = n\bar{f} $，代入后化简得：

\[m(H,t+1) = m(H,t) \times \frac{f(H)}{\bar{f}}\]

假设模式$ H $的适应度比种群平均高$ c\bar{f} $（即$ f(H) = (1+c)\bar{f} $，$ c>0 $代表“优秀”），代入上式：

\[m(H,t+1) = m(H,t) \times \frac{(1+c)\bar{f}}{\bar{f}} = m(H,t) \times (1+c)\]

以此类推，迭代$ t $代后，模式$ H $的数量会变成：

\[m(H,t) = (1+c)^t \times m(H,0)\]

这就证明了： 适应度高于种群平均的模式，在选择操作下会呈指数级增长 。

11 神经网络模拟

11.1 多层神经网络

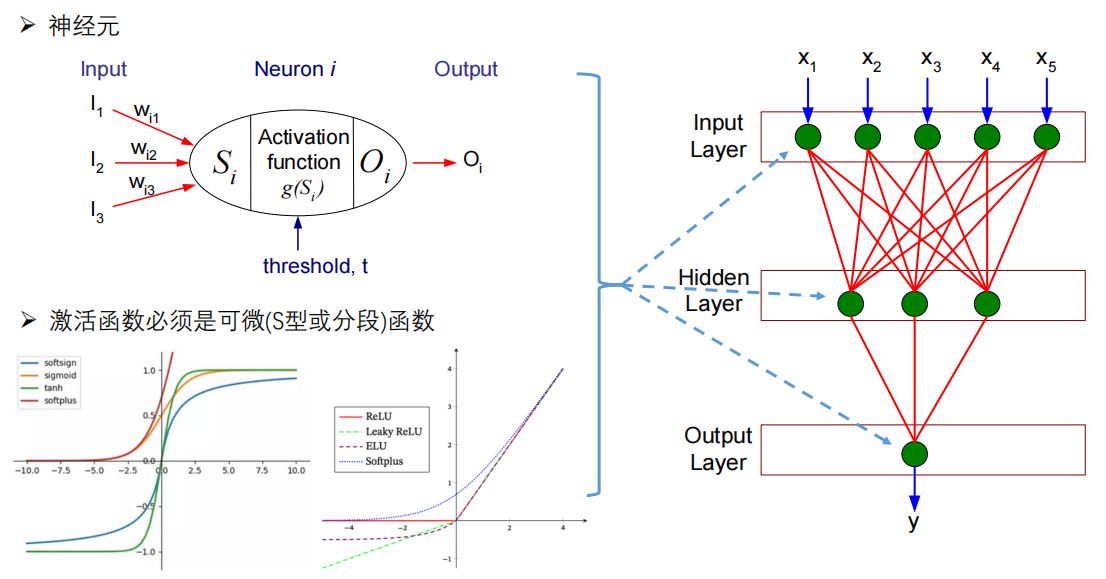
多层神经网络是由许多个“神经元”按照“层级”堆叠而成的数学模型。

多层神经网络的基石是神经元 (Neuron)。

输入 (Input, $I$): 接收来自外界或上一层神经元的信息。
权重 (Weights, $w$): 每个输入都有一个对应的权重（如 $w_{i1}, w_{i2}$），代表该输入对当前神经元的重要性。
加权求和与阈值 ($S_i$): 神经元将所有输入乘以权重后相加，并结合一个阈值 (threshold, t)（通常也称为偏置 Bias），形成总输入 $S_i$。
激活函数 (Activation Function, $g(S_i)$): 这是关键一步。总输入经过这个函数处理，决定该神经元输出什么内容 ($O_i$)。

图右侧展示了如何将上述的“单个神经元”组装成一个多层神经网络。右边的每一个绿色节点（圆形），在内部结构上都等同于左边的那个神经元模型。

这个网络由三部分组成：

输入层 (Input Layer):
- 对应图中的 $x_1$ 到 $x_5$。
- 它是网络的最前端，负责直接接收外部的原始数据，不进行计算，只负责传递信号。
隐藏层 (Hidden Layer):
- 对应中间的一层（图中画了3个节点）。
- 这是“多层”神经网络的核心特征。 它夹在输入和输出之间，对用户是不可见的（所以叫“隐藏”）。它负责提取特征和进行复杂的非线性变换。虽然图中只画了一层，但深层网络可以有几十甚至上百个隐藏层。
输出层 (Output Layer):
- 对应底部的节点，输出 $y$。
- 它负责整合隐藏层的信息，给出最终的预测结果或分类结果。

图中红色的连线代表了全连接 (Fully Connected) 关系：

上一层（如输入层）的每一个节点，都与下一层（如隐藏层）的每一个节点相连。
每一条红线都代表着一个权重 ($w$)。神经网络的“学习”过程，其实就是在不断调整这些红线所代表的数值。

左下角特别强调了激活函数。

为什么需要它？ 如果没有激活函数，无论网络有多少层，最终都只是简单的线性叠加。激活函数引入了非线性因素，让神经网络能够处理复杂的问题（比如识别图片、理解语言）。
特性要求： 图中文字指出，激活函数必须是可微的（即可以求导，这是为了通过反向传播算法来训练网络），常见的形状是S型（如Sigmoid, Tanh）或分段函数（如ReLU, Leaky ReLU）。

11.2 梯度反向传播

简单来说，梯度反向传播是神经网络训练的核心算法。它的目的是告诉神经网络：“你现在的预测错了多少，以及你应该如何调整每一个连接的权重（Weight），才能在下一次预测得更准。”

在一个多层神经网络（MLP）中，信号是从输入层一层层向前传递到输出层的（前向传播）。然而，当网络输出结果与真实结果有偏差（即产生误差）时，我们需要修正网络中的参数。

反向传播就是指：将输出层产生的误差，按照网络连接的路径“反向”传回给前面的每一层，从而计算出每个神经元的权重对总误差“贡献”了多少（即梯度）。

A. 最小化误差函数

误差函数公式： $E = \frac{1}{2} \sum_{i=1}^{N} \left( y_i - \sigma\left( \sum_j w_j x_{i,j} \right) \right)^2$
原理： 首先通过前向传播得到预测值，然后用误差函数 (Error Function) 来衡量预测值与真实值 $y_i$ 之间的差距。
目的： 训练的目标就是找到一组权重参数，使得这个误差 $E$ 最小。

B. 随机梯度下降法

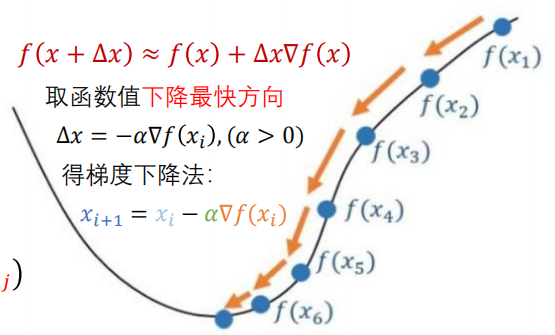
\[\omega_j^{(t+1)} = \omega_j^{(t)} - \lambda \frac{\partial E}{\partial \omega_j}\]

曲线图展示了一个“下山”的过程。横轴是参数（权重），纵轴是误差 $f(x)$。为了让误差最小化，我们需要沿着误差函数下降最快的方向调整参数。这个方向就是梯度的反方向。

图中的公式 $\Delta x = -\alpha \nabla f(x_i)$ 表达的就是：新的位置 = 旧位置 - (学习率 $\times$ 梯度)。就像你在山上（高误差），想要下到谷底（低误差），你会环顾四周，找到坡度最陡峭向下的方向迈出一步。

C. 反向传播机制

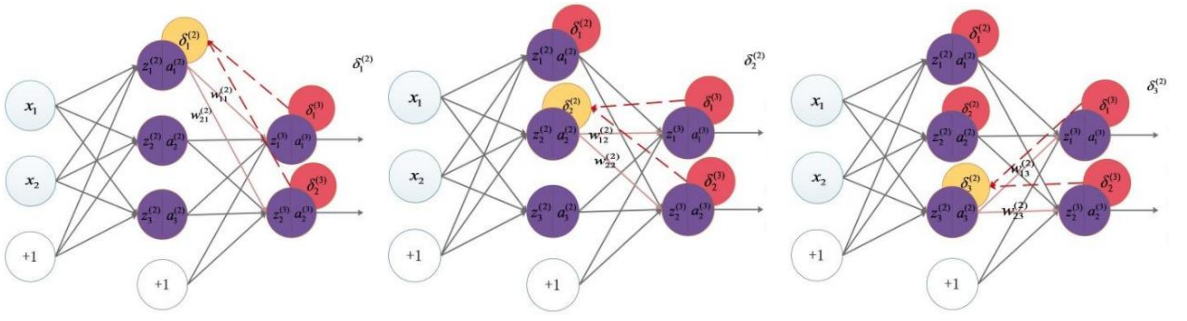
问题： 输出层的误差很容易计算，但对于中间的隐藏层，我们不知道它们到底犯了什么错，因为它们没有直接的“正确答案”。
解决： 利用微积分中的链式法则 (Chain Rule)。
- 公式： 图中的 $\frac{\partial E}{\partial \omega_j} := \delta_j = \sum_i (y_i - x_{i,j}) x_{i,j} \left( 1 - x_{i,j} \right)$ 展示了梯度的计算。
- $\delta$ (Delta) 的传递： 请看底部的三个神经网络示意图。
  - 红色节点代表误差信号 $\delta$。
  - 误差首先在最右边的输出层被计算出来。
  - 然后，这个误差信号沿着红色的虚线反向传递给上一层的神经元。
  - 如果某个连接的权重很大，说明前一个神经元对错误的“贡献”很大，那么它分摊到的误差责任（梯度）也就越大。

案例: 求函数极小值

例1：单变量函数的梯度下降

目标函数： $J(\theta) = \theta^2$
任务： 使用梯度下降法求该函数的极小值。
初始条件：
- 初始点：$\theta_0 = 1$
- 学习率 (Learning Rate)：$\alpha = 0.4$
求解目标： 计算经过三次迭代后的参数值 $\theta_1, \theta_2, \theta_3$。

下面开始求解, 梯度下降的基本公式为：$\theta_{new} = \theta_{old} - \alpha \times \nabla J(\theta)$。首先计算目标函数的导数（梯度）： $J'(\theta) = \frac{d}{d\theta}(\theta^2) = 2\theta$

第 1 次迭代：

当前点：$\theta_0 = 1$
梯度：$J’(1) = 2 \times 1 = 2$
更新公式：$\theta_1 = \theta_0 - \alpha \times J’(\theta_0)$
计算：$\theta_1 = 1 - 0.4 \times 2 = 1 - 0.8 = 0.2$
结果：$\theta_1 = 0.2$

第 2 次迭代：

当前点：$\theta_1 = 0.2$
梯度：$J’(0.2) = 2 \times 0.2 = 0.4$
更新公式：$\theta_2 = \theta_1 - \alpha \times J’(\theta_1)$
计算：$\theta_2 = 0.2 - 0.4 \times 0.4 = 0.2 - 0.16 = 0.04$
结果：$\theta_2 = 0.04$

第 3 次迭代：

当前点：$\theta_2 = 0.04$
梯度：$J’(0.04) = 2 \times 0.04 = 0.08$
更新公式：$\theta_3 = \theta_2 - \alpha \times J’(\theta_2)$
计算：$\theta_3 = 0.04 - 0.4 \times 0.08 = 0.04 - 0.032 = 0.008$
结果：$\theta_3 = 0.008$

结论： 随着迭代进行，$\theta$ 值迅速接近 $0$，即函数 $J(\theta)=\theta^2$ 的真实极小值点。

例2：双变量函数的梯度下降

1. 题目叙述

目标函数： $J(\theta_1, \theta_2) = \theta_1^2 + \theta_2^2$
任务： 使用梯度下降法求该函数的极小值。
初始条件：
- 初始点：$\Theta_0 = (2, 3)$，即 $\theta_1=2, \theta_2=3$
- 学习率 (Learning Rate)：$\alpha = 0.1$
求解目标： 计算前两次迭代后的坐标 $\Theta_1$ 和 $\Theta_2$。

2. 求解过程

首先计算目标函数的梯度向量 $\nabla J$： $\nabla J = (\frac{\partial J}{\partial \theta_1}, \frac{\partial J}{\partial \theta_2}) = (2\theta_1, 2\theta_2)$

第 1 次迭代：

当前点：$\Theta_0 = (2, 3)$
梯度：$\nabla J(2, 3) = (2\times2, 2\times3) = (4, 6)$
更新公式：$\Theta_1 = \Theta_0 - \alpha \times \nabla J(\Theta_0)$
计算：
- $\theta_1$ 更新：$2 - 0.1 \times 4 = 2 - 0.4 = 1.6$
- $\theta_2$ 更新：$3 - 0.1 \times 6 = 3 - 0.6 = 2.4$
结果：$\Theta_1 = (1.6, 2.4)$

第 2 次迭代：

当前点：$\Theta_1 = (1.6, 2.4)$
梯度：$\nabla J(1.6, 2.4) = (2\times1.6, 2\times2.4) = (3.2, 4.8)$
更新公式：$\Theta_2 = \Theta_1 - \alpha \times \nabla J(\Theta_1)$
计算：
- $\theta_1$ 更新：$1.6 - 0.1 \times 3.2 = 1.6 - 0.32 = 1.28$
- $\theta_2$ 更新：$2.4 - 0.1 \times 4.8 = 2.4 - 0.48 = 1.92$
结果：$\Theta_2 = (1.28, 1.92)$

结论： 参数点从 $(2,3)$ 移动到了 $(1.28, 1.92)$，正沿着“碗”的形状向底部的最低点 $(0,0)$ 移动。

例3：神经网络求解函数极小值

1. 题目叙述

目标函数： $f(x) = x_1^2 + x_2^2 + x_3^2$
任务： 利用一个多层神经网络（MLP）来寻找该函数取极小值时的自变量值。
网络架构： 一个四层神经网络，各层神经元个数依次为：
- 输入层：1个
- 隐藏层1：4个
- 隐藏层2：2个
- 输出层：3个（分别对应 $x_1, x_2, x_3$）
输入设置： 输入值固定为 $1$。
输出目标： 输出层的三个值即为我们要寻找的自变量值 $(x_1, x_2, x_3)$。

2. 求解分析与答案

这道题与前两道不同，它不是让你手算迭代，而是描述了一个利用神经网络进行优化的编程任务（PPT最后提到了代码文件 demo_mlp_minfun.ipynb）。

求解原理：

构建网络： 搭建结构为 1 -> 4 -> 2 -> 3 的全连接网络。
定义损失 (Loss)： 这里的“预测”实际上就是我们想求的解。我们将网络的输出定义为 $\hat{y} = [\hat{x}_1, \hat{x}_2, \hat{x}_3]$。我们的目标是让 $f(x)$ 最小，因此直接将损失函数定义为目标函数本身： $Loss = \hat{x}_1^2 + \hat{x}_2^2 + \hat{x}_3^2$
训练过程：
- 向网络输入常数 $1$。
- 网络前向传播输出三个值。
- 计算 Loss。
- 通过反向传播 (Backpropagation) 计算梯度，更新网络的权重和偏置。
- 重复训练，直到 Loss 趋近于 0。

理论上的最终解： 无论神经网络的权重如何初始化，只要训练收敛，对于函数 $f(x) = x_1^2 + x_2^2 + x_3^2$ 来说，其平方和最小的情况只有一种： $x_1 = 0, \quad x_2 = 0, \quad x_3 = 0$

因此，该例题的最终求解结果（神经网络训练完成后的输出）应接近： Output = $[0, 0, 0]$

13 科学计算中的蒙特卡洛

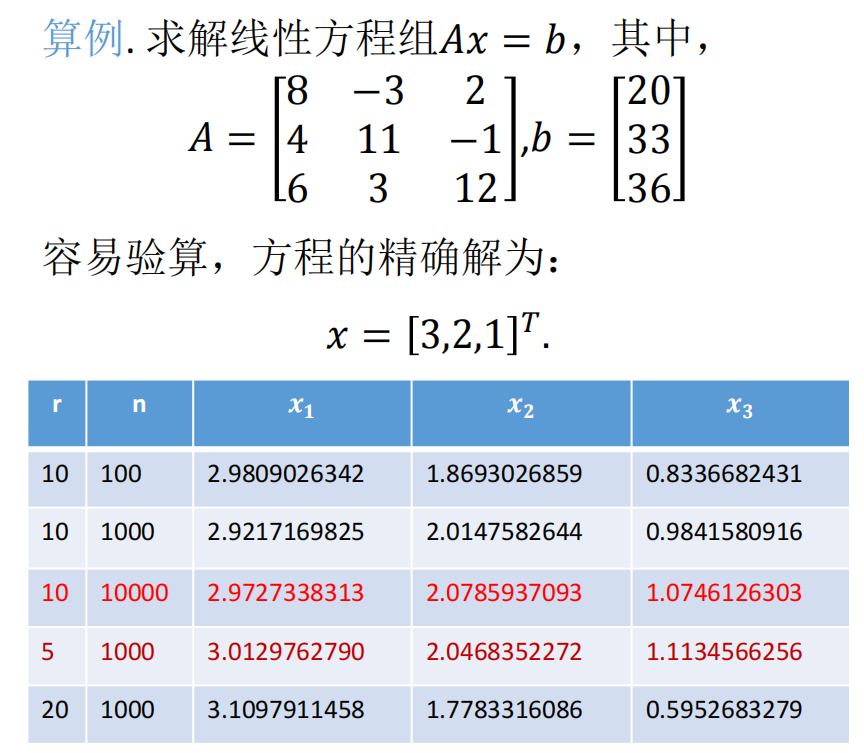
13.1 求解线性方程组$\boldsymbol{Ax = c}$

通常我们解线性方程组使用高斯消元法或迭代法. 下面我们介绍一种概率算法, 通过模拟随机游动来模拟方程组的解.

非奇异矩阵$A = [a_{ij}]$，列向量$\boldsymbol{x} = [x_i]^T$，$\boldsymbol{c} = [c_i]^T$

通过一定变换，得到线性方程组的雅克比迭代形式： $\boldsymbol{x}^{k+1} = B\boldsymbol{x}^k + \boldsymbol{d}$

其中，$B = {b_{ij}}$,并满足收敛条件： $\max_{1 \leq i \leq m} \sum_{j=1}^m |b_{ij}| < 1$

迭代公式可以表示成诺依曼级数( $\boldsymbol{x}$初值取$0$ )： $\boldsymbol{x} = \sum_{k=0}^\infty B^k \boldsymbol{d} = \boldsymbol{d} + B\boldsymbol{d} + \dots + B^k \boldsymbol{d} + \dots$

级数展开, 如果B满足收敛条件, x可以写成一个无穷级数

线性代数方程组第$i$个未知量$x_i$的诺依曼级数解为： $x_i = d_i + \sum_{i_1=1}^m b_{ii_1} d_{i_1} + \sum_{i_1=1}^m \sum_{i_2=1}^m b_{ii_1} b_{i_1i_2} d_{i_2} + \dots + \dots + \sum_{i_1=1}^m \sum_{i_2=1}^m \dots \sum_{i_k=1}^m b_{ii_1} b_{i_1i_2} \dots b_{i_{k-1}i_k} d_{i_k} + \dots$

假设一个具有$m$个状态的马尔科夫链： $i \to i_1 \to i_2 \to \dots \to i_m$

其中$m$个状态之间的转移概率矩阵$P$满足 $\sum_{j=1}^m p_{ij} = 1$

这里取： $p_{ij} = \frac{|b_{ij}|}{\sum_{k=1}^n |b_{ik}|}$

通过概率矩阵$P$和迭代矩阵$B$，可得转移矩阵

\[w_{ij} = \begin{cases} 0, & b_{ij} = 0, \\ \frac{b_{ij}}{p_{ij}}, & b_{ij} \neq 0. \end{cases}\]

13.1.1 雅可比迭代中矩阵B和向量d的确定方法

雅可比迭代是求解线性方程组$A\boldsymbol{x}=\boldsymbol{c}$的经典迭代算法，其核心是将矩阵$A$分解为对角矩阵$D$、严格下三角矩阵$L$和严格上三角矩阵$U$，再通过代数变换推导出迭代格式 $\boldsymbol{x}^{k+1}=B\boldsymbol{x}^k+\boldsymbol{d}$。

一、矩阵A的分解

对于$n$阶非奇异矩阵$A=[a_{ij}]$，可唯一分解为： $A = D + L + U$ 其中：

对角矩阵$D$：仅保留$A$的主对角线元素，$D=\text{diag}(a_{11},a_{22},\dots,a_{nn})$，且$a_{ii}\neq0$（雅可比迭代的前提条件）。
严格下三角矩阵$L$：保留$A$主对角线以下的元素，主对角线及以上元素为0，即当$i>j$时$L_{ij}=a_{ij}$，否则$L_{ij}=0$。
严格上三角矩阵$U$：保留$A$主对角线以上的元素，主对角线及以下元素为0，即当$i<j$时$U_{ij}=a_{ij}$，否则$U_{ij}=0$。

二、雅可比迭代的推导过程

原方程变形：将$A\boldsymbol{x}=\boldsymbol{c}$代入分解式，得到$(D+L+U)\boldsymbol{x}=\boldsymbol{c}$。
分离对角项：将对角矩阵$D$与其他项分离，即$D\boldsymbol{x}=-(L+U)\boldsymbol{x}+\boldsymbol{c}$。
两边左乘$D^{-1}$：由于$D$是对角矩阵且主对角线非零，其逆矩阵$D^{-1}=\text{diag}(1/a_{11},1/a_{22},\dots,1/a_{nn})$，可得： $\boldsymbol{x} = -D^{-1}(L+U)\boldsymbol{x} + D^{-1}\boldsymbol{c}$
构建迭代格式：将上式转化为迭代形式，第$k+1$次迭代值由第$k$次迭代值表示，即： $\boldsymbol{x}^{k+1} = -D^{-1}(L+U)\boldsymbol{x}^k + D^{-1}\boldsymbol{c}$

三、矩阵B和向量d的表达式

对比标准迭代格式$\boldsymbol{x}^{k+1}=B\boldsymbol{x}^k+\boldsymbol{d}$，可直接得到：

迭代矩阵B： $\boldsymbol{B} = -D^{-1}(L+U)$ 其元素$b_{ij}$的具体表达式为： $b_{ij} = \begin{cases} 0, & i=j \\ -\frac{a_{ij}}{a_{ii}}, & i\neq j \end{cases}$ 物理意义：每次迭代时，用前一次迭代的其他分量更新当前分量，权重为对应非对角线元素与主对角线元素的比值的相反数。
常数向量d： $\boldsymbol{d} = D^{-1}\boldsymbol{c}$ 其元素$d_i$的具体表达式为： $d_i = \frac{c_i}{a_{ii}}$ 物理意义：原方程中常数项与对应主对角线元素的比值，是迭代过程中的固定偏移量。

13.1 2 雅可比迭代实例

以二阶线性方程组为例： $\begin{cases} a_{11}x_1 + a_{12}x_2 = c_1 \\ a_{21}x_1 + a_{22}x_2 = c_2 \end{cases}$ 分解矩阵$A=\begin{bmatrix}a_{11}&a_{12}\a_{21}&a_{22}\end{bmatrix}$，则$D=\begin{bmatrix}a_{11}&0\0&a_{22}\end{bmatrix}$，$L+U=\begin{bmatrix}0&a_{12}\a_{21}&0\end{bmatrix}$。计算得： $B=-D^{-1}(L+U)=\begin{bmatrix}0&-a_{12}/a_{11}\\-a_{21}/a_{22}&0\end{bmatrix}, \quad d=\begin{bmatrix}c_1/a_{11}\\c_2/a_{22}\end{bmatrix}$ 迭代格式为： $\begin{cases} x_1^{k+1} = -\frac{a_{12}}{a_{11}}x_2^k + \frac{c_1}{a_{11}} \\ x_2^{k+1} = -\frac{a_{21}}{a_{22}}x_1^k + \frac{c_2}{a_{22}} \end{cases}$ 符合雅可比迭代“每次迭代仅用前一次的全部分量更新当前分量”的核心逻辑。

13.1.3 基于随机游动的计算模型

定义随机变量$e_k$为： $e_k = w_{ii_1} w_{i_1i_2} \dots w_{i_{k-1}i_k} \quad 并且 \quad e_0 = 1$

则随机变量$\theta$定义为： $\theta = \sum_{k=0}^\infty e_k d_{i_k}$

\[w_{ij} = \begin{cases} 0, & b_{ij} = 0, \\ \frac{b_{ij}}{p_{ij}}, & b_{ij} \neq 0. \end{cases}\]

可以验证：$\theta$的期望为$x_i$：

\[\begin{align*} E(\theta) &= d_i + \sum_{i_1=1}^m w_{ii_1} p_{ii_1} d_{i_1} + \sum_{i_1=1}^m \sum_{i_2=1}^m w_{ii_1} p_{ii_1} w_{i_1i_2} p_{i_1i_2} d_{i_2} + \dots + \dots \\ &= \sum_{k=0}^\infty \sum_{i_1=1}^m \sum_{i_2=1}^m \dots \sum_{i_k=1}^m w_{ii_1} p_{ii_2} \dots w_{i_{k-1}i_k} p_{i_{k-1}i_k} d_{i_k} = x_i \end{align*}\] \[x_i = d_i + \sum_{i_1=1}^m b_{ii_1} d_{i_1} + \sum_{i_1=1}^m \sum_{i_2=1}^m b_{ii_1} b_{i_1i_2} d_{i_2} + \dots + \dots + \sum_{i_1=1}^m \sum_{i_2=1}^m \dots \sum_{i_k=1}^m b_{ii_1} b_{i_1i_2} \dots b_{i_{k-1}i_k} d_{i_k} + \dots\]

通过推导发现，这个期望值的展开式，竟然和第一步中那个诺依曼级数展开式一模一样。因此, 只要我们模拟足够多次的随机游动并取平均值，就能求出方程的解 $x_i$。

随机游走算法的思路是：把“矩阵幂 $ B^k $”转化为“随机路径的权重乘积”，再通过大量随机路径的平均，近似诺依曼级数的和。

具体操作（对应代码/公式）：

定义“随机路径”的概率规则 构造概率矩阵 $ P $：$ P(i,j) = \frac{|B(i,j)|}{\sum_{j} |B(i,j)|} $（第 $ i $ 行的元素是从节点 $ i $ 走到节点 $ j $ 的概率）。同时构造权重矩阵 $ W $：$ W(i,j) = \frac{B(i,j)}{P(i,j)} $（路径的“权重”，用来还原 $ B $ 的实际数值）。
随机游走的“路径生成” 从某个初始节点 $ i $ 出发，按照概率矩阵 $ P $ 随机选择下一个节点 $ i_1 $，再从 $ i_1 $ 选 $ i_2 $，……，生成一条随机路径 $ i \to i_1 \to i_2 \to \dots \to i_k $。
路径的“统计量”计算 对这条路径，定义两个统计量：
- 路径权重 $ e_k $：$ e_k = W(i,i_1) \cdot W(i_1,i_2) \cdot \dots \cdot W(i_{k-1},i_k) $（对应 $ B^k $ 中的元素乘积）；
- 累积和 $ \theta $：$ \theta = \sum_{k=0}^{\infty} e_k \cdot d_{i_k} $（对应诺依曼级数 $ \sum B^k d $）。
大量路径的“平均”近似解 重复生成 num 条随机路径，计算每条路径的 $ \theta $，再取这 num 个 $ \theta $ 的平均值，作为 $ x(i) $ 的近似解： $x(i) \approx \frac{1}{\text{num}} \sum_{l=1}^{\text{num}} \theta_l$

为了更好理解，你可以这样想象：你要计算某个城市的繁忙程度（$x_i$）。传统方法是你需要拿到所有城市的交通数据，列一个巨大的方程组并通过中央电脑统一计算。蒙特卡洛方法是你派出 10,000 个虚拟的“随机快递员”从该城市出发。他们根据路况（矩阵 $B$ 转化来的概率 $P$）随机去往下一个城市。每到一个城市，他们就收集一点当地的特产（向量 $\boldsymbol{d}$），并根据路费（权值 $w$）调整手里的总价值。最后，你只需要把这 10,000 个快递员带回来的总价值算个平均数，这个数就是该城市的繁忙程度。

你可能会问，直接解方程不好吗？为什么要在计算机里搞随机模拟？如果你有一个 $10000 \times 10000$ 的超大矩阵，但你只想知道其中第 5 个未知数的值。传统方法必须解出整个方程组，而蒙特卡洛方法只需从第 5 个状态开始模拟即可，极大地节省算力。这种并行计算的方法非常适合超级计算机。因为每一条“随机游动路径”都是互不干扰的，可以同时由成千上万个 CPU 核心分别计算。

13.1.4 随机算法流程

# 初始化
N_sim = 1000  # 模拟次数 (numn)
Max_step = 10 # 游动深度 (numr)
m = 3         # 方程组维数

# 预处理：计算迭代矩阵 B 和向量 d，以及概率矩阵 P 和权重 W
D = diag(A)
B = inv(D) * (L + U)  # 雅可比迭代矩阵
d = inv(D) * b
P = normalize(abs(B), row_wise) # 归一化构造概率
W = B / P                       # 构造权重矩阵

# 求解每个未知数 x[i]
for i from 1 to m:
    Grand_Total = 0  # 用于累加所有粒子的得分

    # 开始 N_sim 次独立的随机游动
    for n from 1 to N_sim:
        
        # --- 单次随机游动开始 ---
        current_state = i
        q = 1           # 初始路径权重乘积 (e_0)
        path_score = 0  # 本次游动的得分 (随机变量 theta)
        
        # 初始项贡献 (级数第0项 d_i)
        path_score = path_score + q * d[current_state] 
        
        # 走 Max_step 步
        for k from 1 to Max_step:
            # 1. 根据概率 P 随机选择下一个状态 next_state
            next_state = random_choice(based_on = P[current_state, :])
            
            # 2. 更新路径权重积 (对应公式 e_k)
            # q_new = q_old * w_{current, next}
            q = q * W[current_state, next_state]
            
            # 3. 累加贡献 (对应公式 sum e_k * d_k)
            path_score = path_score + q * d[next_state]
            
            # 移动到下一状态
            current_state = next_state
        # --- 单次随机游动结束 ---

        Grand_Total = Grand_Total + path_score

    # 计算期望值：总分 / 次数
    x[i] = Grand_Total / N_sim

13.2 椭圆形偏微分方程

13.3 抛物型偏微分方程

13.4 粒子输运模拟-KMC

14 复杂网络与元胞自动机

翘课了，笔记忘记补嘞

冬七周实验课

2随机数发生器, 简单的要会, 线性同余法. 这个部分课本上没有, 着重看PPT, 梅森的流程. 有哪些随机数的检验方法, 随机数检验的概念, 看另外一个教材文件.

3随机性, 基于贝叶斯公式的模拟, 是基本的知识, 概率太深入的东西不会考, 知道期望方差.

4离散事件模拟知道书上的就行. 几个分布的模拟方法.

5特定分布的随机数, 拒绝接受和逆变换方法, 关键是要会用, 会有计算题, 用给定方法从规定分布中抽样.

6 基本蒙特卡洛, 讲积分. 有一部分理论结果, 投点法收敛性, 重要性采样, 分层采样做实验.

7 序贯蒙特卡洛, 除了PPT, 还要看一下重要性采样, 降低方差的基本技巧. 控制变量法与. 理解概念, 后一次在前一次之上

8 mcmc. Metropolis–Hastings 采样和为什么是收敛的. 课本上的例子掌握.

9模拟退火. 在一个玻尔兹曼分布上进行抽样.

10遗传算法. 都是一种优化的方法.

11 神经网络模拟, 要知道应用, 使用神经网络来进行函数逼近. 卷面考试不作为重点. 考察范围仅限于随机微分方程与随机游走有关. 金融相关知道概念即可, 不需要计算.资产定价等会出计算.

12方程求解. 掌握随机游走, 波尔兹曼方程, 仅限于理解了解PPT上内容. 求线性方程组可能会考.

13复杂网络模拟, 看一下课本上的知识.

9 10 13 15 是课本上的, 课本上有的会详细一点, 其他的补充内容可能不涉及计算.

2024-2025秋冬学期考试卷

第一题

1.2

要使用接受-拒绝法生成伽马分布$ f(x)=\frac{2}{\sqrt{\pi}} x^{\frac{1}{2}} e^{-x} $的样本，需遵循以下步骤：

步骤1：确定常数$ M $（满足$ f(x) \leq M g(x) $）

首先计算$ \frac{f(x)}{g(x)} $的表达式（$ g(x)=\frac{2}{5} e^{-\frac{2}{3}x} $是建议分布）： $\frac{f(x)}{g(x)} = \frac{\frac{2}{\sqrt{\pi}} x^{\frac{1}{2}} e^{-x}}{\frac{2}{5} e^{-\frac{2}{3}x}} = \frac{5}{\sqrt{\pi}} x^{\frac{1}{2}} e^{-\frac{x}{3}}$

对$ h(x)=\frac{5}{\sqrt{\pi}} x^{\frac{1}{2}} e^{-\frac{x}{3}} $求最大值（找临界点）：求导并令导数为0： $h'(x) = \frac{5}{\sqrt{\pi}} \cdot e^{-\frac{x}{3}} \left( \frac{1}{2}x^{-\frac{1}{2}} - \frac{1}{3}x^{\frac{1}{2}} \right) = 0$ 解得临界点$ x = \frac{3}{2} $。

将$ x=\frac{3}{2} $代入$ h(x) $，得到$ M $： $M = h\left(\frac{3}{2}\right) = \frac{5}{\sqrt{\pi}} \cdot \left(\frac{3}{2}\right)^{\frac{1}{2}} \cdot e^{-\frac{1}{2}} \approx 2.13$

步骤2：接受-拒绝法抽样流程

生成建议分布的样本$ y $：建议分布$ g(x) $是指数型分布，抽样方法为：取均匀分布$ U_1 \sim \text{Uniform}(0,1) $，则 $y = -\frac{3}{2} \ln(1-U_1)$
生成均匀分布样本$ u $：取$ U_2 \sim \text{Uniform}(0,1) $，记其样本为$ u $。
判断是否接受$ y $：计算接受准则： $h(y) = \frac{f(y)}{M g(y)} = \frac{5}{\sqrt{\pi} M} \cdot y^{\frac{1}{2}} e^{-\frac{y}{3}}$
- 若$ u < h(y) $，接受$ y $，作为伽马分布的样本；
- 若$ u \geq h(y) $，拒绝$ y $，回到步骤1重新生成$ y $和$ u $。