Machine Learning

监督学习：
单变量线性回归与多元线性回归

"Supervised Machine Learning: Linear Regression"

Posted by Summer on February 18, 2025

监督学习:线性回归与逻辑回归(Supervised Machine Learning: Regression and Classification)

1 机器学习绪论

1.1 what is machine learning

机器学习的定义：field of study that gives computers the ability to learn without being explicitly programmed 在没有明确编程的情况下学习

目前常用的两种机器学习算法：

  • 监督学习（Supervised learning）
  • 无监督学习（Supervised learning）

Reinforcement learning 强化学习，是另一种机器学习

1.2 监督学习(Supervised learning)

FIGURE:learn from given “right answer”

input(x) $\rightarrow$ output label(y)

最终接受只有输入没有输出（“right answer”），给出合理预测

  • 回归算法(regression algorithms),例如根据房价预测；回归试图预测无限多可能的数字中的任意一个

  • 分类算法(classification algorithms)，例如breast cancer detection 恶性的肿瘤malignant，还是良性的benign；分类只有n种可能的输出,predict categories,是猫还是狗.需要找到分类的边界

    案例:given email labeled as spam/not spam,learn a spam filter

1.3 无监督学习(Unsupervised learning)

定义:data only comes with inputs x, but not output labels y

Algorithm has to find structure in the data

给定的数据与任何输出标签y无关，我们的工作是找到一些结构或者模式，或者只是在数据中找到有趣的东西

  • 类聚算法(clustering algorithm),将未标记的数据放入不同的集群中;在没有监督的情况下寻找分类,group similar data points together.
    • 案例1：given a set of news articles found on the web,group them into sets of articles about the same story.熊猫的新闻中出现了panda,zoo,japan等等词，类聚算法会将他们自动查找并归类；一天有很多新闻，算法可以无监督地寻找归类cluster。
    • 案例2:given a database of customer data,automatically discover market segments and group customers into different market segments

  • 异常检测(Anomaly detection):find unusual data points

  • 降维(Dimensionality reduction):将大数据集压缩维小数据集同时尽可能丢失少的信息

1.4 Jupiter notebook

运行代码：按住 Shift 键并按 ‘Enter’

2 单变量线性回归

单词 释义 单词 释义
hypothesis 假设函数 Linear regression 线性回归
Parameter 模型参数 cost function 代价函数
Gradient descent 梯度下降 convex function 凸函数

2.1 线性回归模型(Linear Regression Model)

数据集被称作训练集(data set)

Notation:

  • m = Number of training examples →训练样本的数量
  • x’s = “input” variable / features →输入变量 / 特征
  • y’s = “output” variable / “target” variable →输出变量 / 目标变量
  • (x, y) = single training example →一个训练样本
  • ($ x^{(i)}$,$ y^{(i)}$) = ith training example →第i个训练样本

2.2 Cost function 成本/损失函数

Model模型：$ f_{\mathbf{w},b}(\mathbf{x}^{(i)}) = \mathbf{w} \cdot \mathbf{x}^{(i)} + b $

Parameter参数: $\mathbf{w},\mathbf{X}$

Cost function成本函数：

$J(\mathbf{w},b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})^2 $

Objective目标: 使成本函数$J(\mathbf{w},b)$最小

2.3 Gradient descent 梯度下降

2.3.1 什么是梯度算法

梯度下降是用来找到$J(\mathbf{w},b)$最小值的算法

  1. 随机从$w$和$b$的某个值出发
  2. 一步一步下山直至收敛到局部最低点
  3. 梯度下降算法的特点：不同的起始点出发会到达不同的局部最小值(local minima)

2.3.2 梯度算法表达式

下面我们来实现梯度下降(Gradient descent)的算法

多个变量的梯度算法：(重复执行直到满足收敛条件为止)

\[\begin{aligned} \text{repeat}&\text{ until convergence:} \; \lbrace \newline\; & w_j = w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \; & \text{for j = 0..n-1}\newline &b\ \ = b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \newline \rbrace \end{aligned}\]

在这个等式中，$\alpha$是学习率(learning rate)，通常是0~1之间的小正数。如果$\alpha$非常大，说明正在采取非常激进的下坡方式，每一步迈得很大。

事实上，学习率不能过小或过大。

  • 如果学习率过小，每一步都很小，程序会很慢
  • 如果学习率过大，程序一步就会迈过极小值，会越来越发散

2.3.3 Simultaneous update 同步更新

正确的更新方式：

\[\begin{aligned} & temp_w = w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \; & \text{for j = 0..n-1}\newline &temp_b \ = b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \newline & w = temp_w \newline & b = temp_b \end{aligned}\]

下面这个是错误的更新方式：

\[\begin{align*} & temp_w = w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \; & \text{for j = 0..n-1}\newline & w = temp_w \newline &temp_b \ = b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \newline & b = temp_b \end{align*}\]
  1. 更新方程时需要同时更新$w$和$b$
  2. 正确方法：先同时计算右边部分，然后同时更新$w$和$b$
  3. $\times$错误方法：先计算temp0然后更新θ_0，再计算temp1然后更新θ_1

2.4 Gradient descent for linear regression线性回归中的梯度下降算法

  • 线性回归中不会出现多个极小值，三维图像永远是碗形，即convex function
  • bashed gradient descent指的是在梯度下降的每一步中，我们都在查看所有的训练事例，使用了整个训练集（因为有求和）

3 Multivariate linear regression 多元线性回归

名词翻译

单词 词义 单词 词义
feature 特征 Multivariate linear regression 多元线性回归
Feature Scaling 特征缩放 Example automatic convergence test 自动收敛测试
Polynomial regression 多项式回归 Normal equation 正规方程

3.1 Multiple features 多元线性回归

多元线性回归：即有多个特征的线性回归

  • n = number of features →训练样本的数量
  • $\overrightarrow{x}^{(i)}$ = input features of ith training example →第i个训练样本的输入特征值,在多元特征中，$\overrightarrow{x}^{(i)}$是一个一维向量，即一行多列
  • $x_j^{(i)}$ = value of feature j in ith training example →第i个训练样本中第j个特征值

3.2 多元线性回归的梯度下降

3.2.1 常规解法

\[\begin{align*}\text{Parameters }&\overrightarrow{w} = [w_1 \ w_2 \ ...\ w_n] \newline &b\text{ \ still a number} \newline \text{model }& f_{\overrightarrow{w},b}(\mathbf{x})=\overrightarrow{w}\cdot\overrightarrow{x}+b \newline \text{cost function \ } &J(\overrightarrow{w},b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{\overrightarrow{w},b}(\mathbf{x}^{(i)}) - y^{(i)})^2 \newline \text{Gradient decent }& w_j = w_j - \alpha \frac{\partial J(\overrightarrow{w},b)}{\partial w_j} \; \text{for j = 0..n-1} \newline & b = b - \alpha \frac{\partial J(\overrightarrow{w},b)}{\partial b} \end{align*}\]

3.2.2 Normal equation 正规方程 (只适用于线性回归)

  • 提供了一个求最小值的解析解法
  • 正规方程不需要学习率，不用迭代
  • 正规方程速度较慢

3.3 Feature Scalling 特征缩放

3.3.1 特征缩放可以使梯度更快收敛

当一个案例有不同的特征,他们具有不同的值的范围，会导致梯度下降运行缓慢

例如，在房价预测中，房间面积$x_1$为2000，房间数量$x_2$为5，最终价格300k 参数$w_1=0.05$，参数$w_2=50$，参数$b=50$，等高线是椭圆，做梯度下降会运行缓慢 假如对$x_1 ,x_2$做缩放，使得范围相近，等高线变为圆形，加快梯度下降

因此,我们需要特征缩放,来使得特征调整到相似的尺度范围

3.3.2 Mean normalization 均值归一化

方法1.除以最大值

$x_1$在区间[a,b]中,$x_2$在区间[c,d]中

归一化后，$\widehat{x_1}=\frac{x_1}{b}$，$\widehat{x_2}=\frac{x_2}{b}$

方法2. Mean normalization

$x_1$在区间[a,b]中,$x_2$在区间[c,d]中

计算得到$x_1$的平均值$\mu_1$，$x_2$的平均值$\mu_2$

归一化后，$\widehat{x_1}=\frac{x_1-\mu_1}{b-a}$,$\widehat{x_2}=\frac{x_2-\mu_2}{d-c}$

此时$\widehat{x_1}$和$\widehat{x_2}$在(-1,1)内部

方法3. Z-score normalization Z分数归一化

求出平均值$\mu_1$和标准差(standard deviation)$\sigma_1$

归一化后，\(\widehat{x^{(i)}_j} = \dfrac{x^{(i)}_j - \mu_j}{\sigma_j}\)

其中， \(\begin{align*} \mu_j &= \frac{1}{m} \sum_{i=0}^{m-1} x^{(i)}_j \newline \sigma^2_j &= \frac{1}{m} \sum_{i=0}^{m-1} (x^{(i)}_j - \mu_j)^2 \end{align*}\)

注意${x^{(i)}_j}$表示第i个训练样本的第j个特征

在z分数归一化后,所有要素的平均值为0,标准差为1

3.4 检查梯度下降是否收敛

方法一:画一张图

方法二:Automatic convergence test

令$\epsilon = 10^{-3}$

如果在一次迭代中，$J(\overrightarrow{w},b) \leq \epsilon$

那么可以认为收敛

3.5 选择合适的学习率

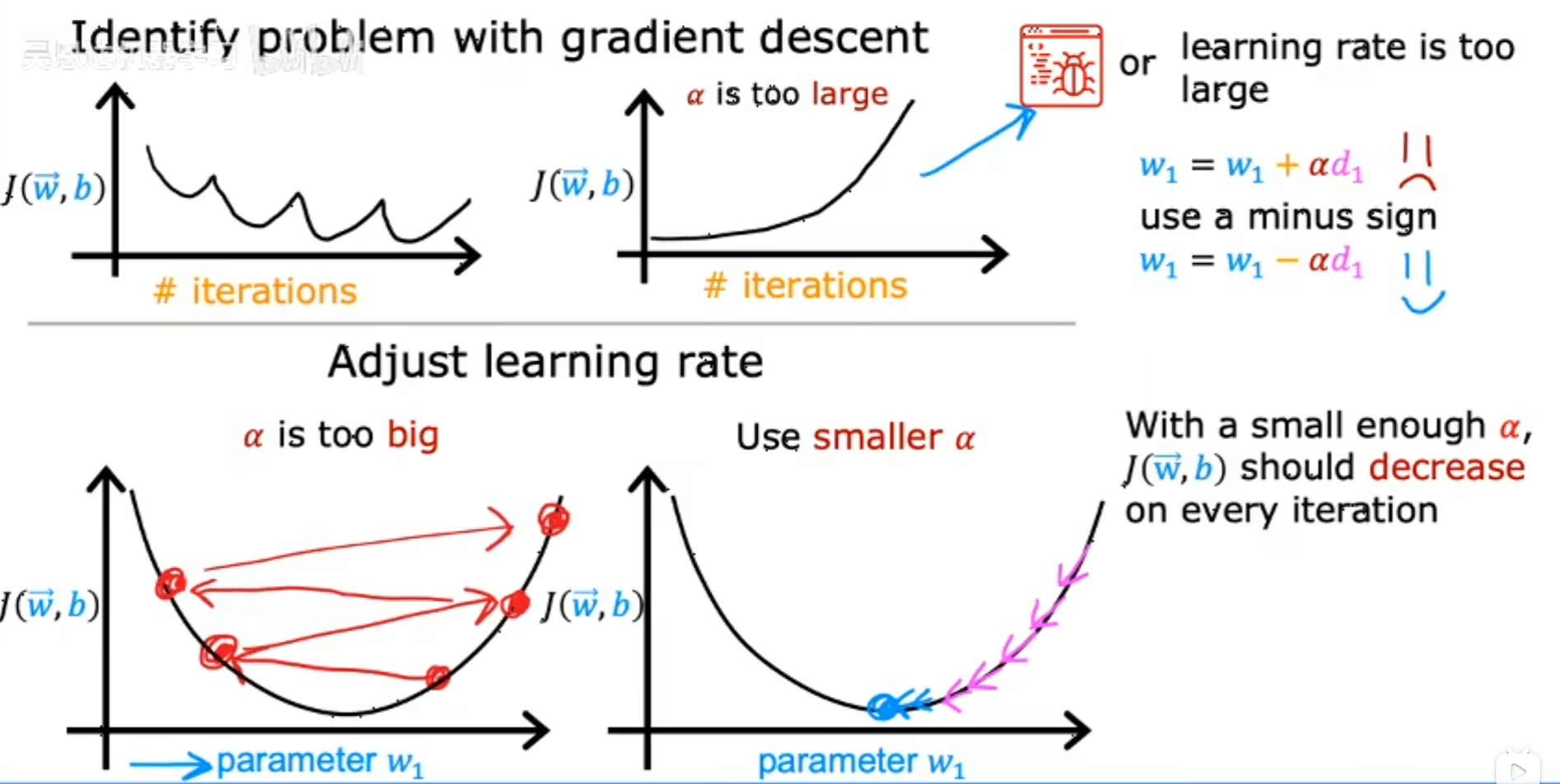
选择合适的学习率

一个debug小技巧,把$\alpha$设置的很小,来检查成本函数是否会下降

如果此时成本函数仍然上升,说明程序中有bug

反复尝试0.001,0.01,0.1,1等数值,选择下降较快的学习率

3.6 Feature Engineering 特征工程

可以根据现实情况,组合原本的特征

例如在房价预测中,地块长度$x_1$,宽度$x_2$,原本的函数为 \(f_{\overrightarrow{w},b}=w_1x_1+w_2x_2+b\) 然而我们知道地块面积$x_3=x_1x_2$也与房价有关,函数变为 \(f_{\overrightarrow{w},b}=w_1x_1+w_2x_2+w_3x_3+b\) 这就是特征工程

特征工程主要包括

  • 特征选择:从众多特征中选择出最具代表性和区分性的特征，以减少特征维度，提高模型效率和泛化能力。常见的方法有过滤法（如方差分析、相关系数法）、包装法（如递归特征消除法）和嵌入法（如基于 L1 正则化的特征选择）。
  • 特征构建:结合领域知识，通过对现有特征进行组合、变换等操作，创建新的特征。例如，在电商数据分析中，可以根据用户的购买时间和购买金额构建平均购买单价、购买频率等新特征。

3.7 多项式回归(Polynomial regression)

3.7.1 多项式回归的概念

多项式回归是线性回归的扩展，通过增加自变量的高次项来拟合数据，能处理非线性关系。模型形式为 $y = \theta_0 + \theta_1x + \theta_2x^2 + \cdots + \theta_nx^n$

  • 实质是将原始特征 $x$ 转换为包含高次项的特征矩阵 $[x, x^2, \cdots, x^n]$。
  • 能拟合复杂的非线性关系，灵活性高。
  • 容易过拟合，尤其当多项式次数过高时。

3.7.2 代码实例

import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split

# 生成示例数据
np.random.seed(0)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.random.randn(80) * 0.1

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 多项式特征转换,使用PolynomialFeatures将原始特征转换为多项式特征
degree = 3  # 多项式次数
poly = PolynomialFeatures(degree=degree)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.transform(X_test)

# 线性回归拟合
model = LinearRegression()
model.fit(X_train_poly, y_train)

# 预测
y_pred = model.predict(X_test_poly)

# 评估模型,使用 mean_squared_error 和 r2_score 评估模型性能
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"均方误差 (MSE): {mse}")
print(f"决定系数 (R^2): {r2}")

3.8 利用Scikit-Learn进行回归

3.8.1 线性回归模型(LinearRegression)

# 导入numpy库和sklearn库
import numpy as np
from sklearn.linear_model import LinearRegression

# 导入数据
X_train = np.array([[1], [2], [3], [4], [5]])
y_train = np.array([2, 4, 6, 8, 10])

# 创建并训练线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)

# 待预测的数据
X_test = np.array([[6], [7]])

# 使用predict函数进行预测
y_pred = model.predict(X_test)
print("预测结果:", y_pred)

3.8.2 逻辑回归模型(LogisticRegression)

import numpy as np
from sklearn.linear_model import LogisticRegression

# 训练数据
X_train = np.array([[1], [2], [3], [4], [5]])
y_train = np.array([0, 0, 1, 1, 1])

# 创建并训练逻辑回归模型
model = LogisticRegression()
model.fit(X_train, y_train)

# 待预测的数据
X_test = np.array([[6], [7]])

# 进行预测
y_pred = model.predict(X_test)
print("预测结果:", y_pred)

3.8.3 决策树模型(DecisionTreeClassifier)

import numpy as np
from sklearn.tree import DecisionTreeClassifier

# 训练数据
X_train = np.array([[1], [2], [3], [4], [5]])
y_train = np.array([0, 0, 1, 1, 1])

# 创建并训练决策树分类器
model = DecisionTreeClassifier()
model.fit(X_train, y_train)

# 待预测的数据
X_test = np.array([[6], [7]])

# 进行预测
y_pred = model.predict(X_test)
print("预测结果:", y_pred)
CATALOG
    FEATURED TAGS
    Meta Machine Learning Mathematical Modeling
    FRIENDS